Глава 7 Использование математики

We use cookies. Read the Privacy and Cookie Policy

Глава 7

Использование математики

Перспектива, астрономия, музыка, космография, астрология, статика, антропография… гелиоскопия, гидрогогия, зография, архитектура, навигация, тавматургия и архимастрия[125].

Когда Генри Биллингсли, выпускник университета и успешный лондонский торговец, в 1570 году опубликовал первое английское издание, он предложил знаменитому английскому математику Джону Ди написать предисловие о преимуществах и достоинствах математики. Биллингсли и Ди надеялись пробудить математическое воображение, напомнить практикам, насколько необходимо изучение математики для всех прикладных искусств, так же как для изучения природы. Математика не только использовалась во всех прикладных науках, которые Гилберт с удовольствием перечислил в предисловии. Математика в глазах практика XV и XVI веков была не просто абстрактным искусством для специалистов. Для него, как и для греков, термин означал все важные и многочисленные науки и их практическое применение.

Геометрия – отрасль математики, наиболее ценимая греками. Но они не отвергали и другие. Пифагорейцы считали, что математика состоит из четырех разделов: геометрия, арифметика, астрономия и музыка. Они были уверены, что астрономия – это прикладная геометрия, а музыка – прикладная арифметика. Такая классификация продолжала существовать долго, в том числе в виде квадривиума[126] в средневековом университете. Платон, находясь под влиянием пифагорейцев, подчеркнул роль математики в науке и в философии. Чистая математика, по Платону, касавшаяся мира совершенных неизменных абстрактных идей, была наилучшим возможным способом обучением философа, который желает познать природу идей, форм и сущностей. Математика отражает неизменную реальность, стоящую за постоянным движением и неопределенностью мира чувств. Поэтому для платониста изучение природы было поиском математических законов, которые управляют миром. Хотя Аристотель утверждал, что величина и тело – разные вещи, равно как и математика и натурфилософия, платонистская традиция продолжала существовать и привлекать многие умы. Усиление интереса к доктринам платонизма и неоплатонизма в XV веке поддержало идею о том, что математика – ключ не только к науке, но и к большей части того, что в XVII веке называли натурфилософией. Достаточно вспомнить, что Коперник писал для математиков и вполне мог назвать свою книгу «Математические принципы небесного вращения», дабы понять, как антиаристотелианство века выражалось попыткой трактовать математически все то, что Аристотель трактовал качественно.

Платонизм имел огромное влияние на математику Ренессанса. Он, несомненно, поддержал изучение чистой математики и поиск ранее отвергнутых греческих математических текстов. Он также стимулировал введение должностей преподавателей математики в новых гуманистических школах, которые создавались как лингвистические центры. Платоновские традиции помогли возродить должности профессоров математики в университетах, правда, не повлияли на их заработок. Предполагалось, что математика – лучшая тренировка для ума, чем диалектика. Существовали разные полезные аспекты математики, пригодные для неакадемического образования: фортификация для военных людей, геодезическая съемка местности для землевладельцев, практическая астрономия и картография. Если же говорить о менее рациональных аспектах, платонизм и неоплатонизм способствовали такому сильному всплеску нумерологического мистицизма и астрологии, что для широкой аудитории «математик» и «астролог» стали синонимами. (Так и было, когда математиками были Кардан или Ди.) Многие молодые люди, такие как Фернель, должно быть, продвинулись от элементарной геометрии и доктрины сфер до чудес астрологических предсказаний. И не важно, что заботливые отцы вроде Винченцо Галилея предостерегали сыновей об опасностях этого предмета, имеющего сомнительную репутацию и не дающего никакой отдачи.

На математику оказали сильное влияние, во-первых, популяризация науки и, во-вторых, новое осознание нужд техников. В средневековом университете все студенты посещали лекции о Евклиде. Теперь они ожидали от профессоров математики более широкого охвата предмета, от доктрины сфер до использования математики в военном деле, навигации и инженерии. Математики стремились внедрить математику в практику – научить торговца правильно подсчитывать свои доходы и показать изготовителю инструментов, как следует правильно градуировать шкалы приборов. Потребность в математике оказалась настолько велика, что даже появилась новая профессия – математика-практика, человека искусного в практических аспектах математики, который знает, как использовать геометрию и тригонометрию в научных измерительных приборах. Такие люди читали математические лекции на местных языках – эта практика была особенно распространена в Лондоне во второй половине XVI века – и писали элементарные инструкции в простом и понятном изложении.

Хороший пример A Booke Named Tectonicon Леонарда Диггеса, опубликованная в 1556 году и много раз переизданная. Диггес утверждал, что хотел написать «книгу, содержащую цвет наук математических, широко применяемых на практике, выгодную и приятную для всех людей дела в этом королевстве». Пока книга готовилась, он выпустил труд меньшего объема, в котором, как утверждал автор, кратко излагались всевозможные точные измерения и быстрые расчеты земли, площадей, леса, камней, колоколен, столбов, шаров и т. д. В ней рассказывается об изготовлении и использовании плотницкой линейки и ряда других инструментов. Также в ней есть вещи приятные и полезные для землемеров… плотников, каменщиков и людей других профессий.

Иными словами, это учебник математики и для образованных, и для необразованных людей.

Пример ранних попыток применения математики в ремеслах – «Курс искусства измерений с компасом и линейкой» (Course in the Art of Measurement with Compass and Ruler, 1525). Его автор – художник Альбрехт Дюрер (1471–1528). Это пример зографии Ди – применение математики в искусстве. Художники незадолго до этого решили проблему перспективы и метода создания иллюзии трехмерности на двухмерном полотне. Результаты примерно за полувековой период приведены в труде Жана Пелерина «Об искусственной перспективе» (On Artificial Perspective, 1505). Теперь многие художники хотели знать математику и теорию искусства «фальшивой перспективы». Не то чтобы математика могла научить их рисовать, но людям было любопытно узнать профессиональные секреты. Отсюда изучение Леонардо математических пропорций и замысловатые трактаты Дюрера, сделавшего латинские и итальянские знания доступными для немцев. Дюрер не сомневался, что «геометрия – правильная основа любой живописи» и строительства и должна быть доступной для всех.

Не все прикладные математики были заняты обучением ремесленников. Очень многие интересовались математическим фоном теоретических наук. Работа астрономов XV века наглядно продемонстрировала необходимость подробного математического анализа астрономических проблем. Это была работа для специалистов. На более элементарном уровне находилась геометрия сфер, которая помогала подвести и под элементарную астрономию математическую основу. Многие наставники начинали с древних. Линакр, к примеру, использовал собственный перевод Прокла (1499), чтобы преподать детям английской королевской семьи начала астрономии. Другие авторы предпочитали писать новые трактаты, в которых делался акцент на земной сфере, а не на небесной, и они становились географическими, а не астрономическими. Широко распространенным предметом стала космография. Космографические трактаты были самыми разными, начиная от сугубо научных математических трудов таких ученых, как Петер Апиан, профессор математики из Ингольштадта, или Оронс Фине (1494–1555), профессор математики Французского королевского колледжа, до намеренно упрощенных, популярных работ Себастьяна Мюнстера (1489–1552), который получил образование в Гейдельберге и впоследствии читал лекции в Базеле. Все они помогали общему пониманию важности математики.

Навигационные проблемы, которые пытались решить астрономы XV века, все еще находились в сфере деятельности прикладных математиков. Более эрудированные и лучше понимающие нужды моряков профессора математики, так же как и их предшественники, старались найти новые методы для помощи морякам. Они смело подходили к проблеме определения долготы. Апиан и Фине предложили определять широту по «методу лунных расстояний», который предполагал измерение углового расстояния до Луны от определенных звезд, что, в свою очередь, требовало дальнейшего изучения движений Луны и точных таблиц. Но в целом метод был более обещающим, чем хронометраж лунных затмений, недостаточно частых, чтобы быть полезными на практике. Фризиус Гемма (1508–1555), ученик Апиана, профессор математики в Лёвене, предложил использовать часы для определения долготы. Это было фантастически оптимистичное предложение, учитывая современную неточность часов. Жак Бессон, профессор математики в Орлеане, изобрел универсальный инструмент для использования в навигации, астрономии и определения времени, который описал в труде Le Cosmolabe ou Instrument Universel concemant toutes Observations qui se peuvent faire Par les Sciences Mathematiques, Tant au Ciel, en la Terre, comme la Mer (1567). Туда он включил красивое изображение наблюдателя, сидящего на неправдоподобно большом стуле, установленном на кардановом подвесе, чтобы минимизировать помехи из-за качки судна. Как моряки должны найти для этого место на палубе, автор не уточнил.

Все эти методы, хотя и возможные на берегу, были слишком сложными и неточными для использования в море. Неудивительно, что практики, такие как Симон Стевин и Роберт Норман, считали университетских профессоров неудачными наставниками, хотя их собственные методы были немногим лучше. Те же, кому довелось побывать в море, категорически отвергали все предложения. Роберт Хьюз (1553–1632), выпускник Оксфорда и профессиональный математик, имел некоторое право выступать от имени опытных моряков, поскольку сопровождал Томаса Кавендиша в кругосветном путешествии в 1586–1588 годах. Он был полон презрения к математикам, которые предлагали определять долготу по лунным движениям, называя этот способ неточным и рискованным, связанным с множеством трудностей. Другие предлагаемые способы, по его мнению, также непригодны для практического применения на море[127].

Но Хьюз ничего не предложил взамен, кроме использования картографии; практик, объединив силы с приверженцем естественной магии, так же подвержен ошибкам, как математик, – оказалось, что стрелка компаса меняет свое склонение и наклонение со временем и не в состоянии помочь решить проблему.

Несмотря на хитроумные предложения, хорошие таблицы и усовершенствованные инструменты (например, бакстафф[128], описанный Джоном Дэвисом в «Секретах моряков» (Seamen’s Secrets, 1594), мореходы в конце XVI века, равно как и в его начале, предпочитали полагаться на плавание по счислению с помощью небесных светил, если это было возможно. Но и здесь у математиков нашлось несколько полезных советов, не все из которых были приняты. Образованные люди знали, что самое короткое расстояние между двумя точками на земном шаре проходит по дуге большого круга, но моряки обычно предпочитали метод параллельного плавания, или следования по широте. При этом судно двигалось к нужной широте так прямо, как позволял ветер и течение, а потом шло на запад или на восток, пока в поле зрения не появлялась земля. В высшей степени полезным оказалось изобретение лага для измерения скорости судна, с помощью которого можно было подсчитать дневной путь. Английское изобретение, оно очень долго оставалось английской монополией, хотя в конце концов его описал в своей книге Уильям Боурн. Он был моряком и умел оценивать скорость судна, бросив в воду щепку и наблюдая, как она плывет вдоль судна, а сам шагал по палубе, отмечая время. Теперь моряк бросал в воду с кормы бревно, привязанное к канату с узлами, завязанными через равные промежутки, и считал, сколько узлов будет вытравлено за определенное время, которое измерялось песочными часами. Отсюда практика измерения скорости судна в узлах, поскольку расстояние между узлами было подсчитано так, чтобы измерить скорость в одну морскую милю в час. Для точности узлы следовало расположить на правильном расстоянии друг от друга и тщательно проверить часы. Два измерения подряд, как правило, не производились. Но когда длина градуса земной дуги (которая и определяла морскую милю) была далека от точной, моряки обычно не волновались, если отставали. Они говорили, что лучше отстать на расстояние дневного пути от расчетного положения, чем опередить его на расстояние пушечного выстрела.

У математиков всегда были наготове советы. Эдвард Райт, математик, получивший образование в Кембридже и познакомившийся с практической навигацией во время экспедиции на Азорские острова в 1589 году, первым отметил желательность измерения земной поверхности, чтобы с некоторой степенью точности определить длину земного градуса. Он же предложил ряд усовершенствований, основанных на астрономических наблюдениях. Первое измерение в Англии было произведено Ричардом Норвудом (1590–1675) – моряком, учителем математики и землемером. Он измерил шагами расстояние между Лондоном и Йорком и опубликовал результаты в 1637 году в морском справочнике. Существенные усовершенствования таблиц, методов расчета и инструментов произошли в начале XVII века. Следует отметить использование сектора Гюнтера (впервые описанного в 1607 г.), инструмента, который существенно снизил объем расчетов при счислении пути.

Как бы ни определяли местонахождения судна в море – счислением или астрономическими методами (ставшими очень сложными, поскольку разные математики составляли разные таблицы, разрабатывали свои методы и печатали книги), мореходы все равно использовали карты. К началу XVI века почти все сухопутные карты основывались на том или ином виде проекций, но на море преобладали «плоские карты». На плоских картах расстояния между меридианами были одинаковыми на всех широтах, все равно у экватора или у полюса, поэтому в высоких широтах были большие ошибки. Португальский математик Педро Нуньес (1502–1578), последователь Закуто в интересе, проявляемом к использованию математики для совершенствования навигационных методов и техник, сделал попытку проанализировать проблему математически. В 1537 году он опубликовал труд Tracts. Его анализ стал более известным, когда в 1566 году вышла латинская версия работы под названием «Об искусстве мореплавания» (On the Art of Sailing). Нуньес пришел к выводу, что на сфере линия румба или локсодромия (линия одинаковых компасных курсов) – не прямая, как на плоскости, а спираль, заканчивающаяся на полюсе. Он также отметил, что, поскольку меридианы на глобусе сходятся, на морской карте они не должны располагаться на одинаковых расстояниях друг от друга. Соответственно, Нуньес изобрел квадрант, который помог ему установить число лиг в градусе вдоль каждой параллели, однако он не сумел решить значительно более важную математическую задачу – найти проекцию, которая даст требуемую сходимость и сделает румбы прямыми.

Впоследствии об этом писали многие авторы книг по математической навигации, однако следующий реальный шаг к решению проблемы сделал Джерард Меркатор (1512–1594). Меркатор изучал математику у Фризиуса Геммы и читал лекции в Лёвене до тех пор, пока протестантская вера не вынудила его сменить место жительства. Он уехал в Германию, где стал изготавливать измерительные инструменты, составлять карты и делать глобусы. Его глобусы отражают математический гений автора и его знакомство с работами Нуньеса – на некоторые из них он наносил его спираль – локсодромию. Он также вычислил правильное соотношение между длиной и шириной полос, которые наклеиваются на глобус. Разделил свою карту на двенадцать полос, отрезал каждую за двадцать градусов до полюса и сделал еще два круглых лоскута для полюсов. Так достигалась большая степень точности, чем при использовании предыдущих методов. Его карта мира 1569 года, не настоящая морская карта, но, по всей видимости, предназначенная для использования моряками, отражала и другие идеи Нуньеса. Здесь Меркатор раздвинул меридианы ближе к полюсам, очевидно наугад, хотя мог и воспользоваться тригонометрическими методами. Он так и не объяснил, как получил свои фигуры. Другие могли восхищаться его работой, но не могли ее повторить. А Меркатор больше не изготавливал таких карт.

Следующим картографом, напечатавшим карту на основе проекции Меркатора, был голландец Йодокус Хондиус (1563–1611), которых использовал работы английских математиков, будучи в Лондоне в статусе беженца в 1584–1595 годах. Английские математики лучше справились с проблемой, чем Меркатор. Их вдохновителем был Джон Ди, который в 1547 году специально ездил в Бенилюкс, чтобы поговорить с умными людьми, в первую очередь с математиками. Среди последних были Фризиус Гемма и Меркатор. Ди даже привез в Англию несколько глобусов Меркатора. Годом позже Ди снова вернулся на континент, сначала ненадолго, когда был студентом в Лёвене, потом учителем математики в Париже. Здесь он познакомился с Фине, Фернелем и многими другими выдающимися умами современности, приобрел репутацию способного математика и установил переписку с Нуньесом. Таким образом, Ди был в курсе, как обстоят дела в навигации и картографии. Двое его коллег Томас Гариот (1560–1621) и Эдвард Райт утверждали, что добились успеха с локсодромическими картами. Гариот кратко обсудил проблему в пятой части «Трактата о сферах» Хьюза (1594), однако он не указал ни точной информации, ни метода. Первое настоящее обсуждение имело место в трактате Эдварда Райта «Некоторые ошибки в судовождении, проистекающие из ошибок морских карт, приборов и таблиц» (Certaine Errors in Navigation, Arising either of the ordinarie erroneous making of the Sea Chart, Compasse, Cross staff and Tables of declination of the Sunne and fixed

Starres detected and corrected, 1599). Райт не спешил публиковать свой труд; вероятно, он был согласен с Ди в том, что математические знания были эзотерическими и должны были оставаться тайными, хотя он и не разделял увлеченности Ди магическими науками. Труд Райта довольно долго оставался в рукописи, но в конце концов был напечатан. Причем автор заявил, что решился на публикацию только с тем, чтобы помешать его пиратскому изданию под другим именем. Ему действительно было известно, что Хондиус воспользовался его работой, не указав автора, хотя он показал голландцу свои таблицы, взяв с него обещание хранить их в тайне[129]. Если уж его работе предстояло стать всеобщим достоянием, это следовало сделать по всем правилам.

Райт намеревался проанализировать типичные ошибки, как правило связанные с обычными методами счисления. В первую очередь он разобрал ошибки, связанные с использованием плоских карт, определил их геометрические и физические источники и способы их избежать. Райт составил таблицы румбов и показал, как применять таблицы и новые карты, основанные на них, как найти расстояния от одной точки до другой с помощью карт и как лучше всего прокладывать курс. В общем, это было все, что необходимо знать практику, и нудные расчеты были сведены к минимуму. Неудивительно, что Хондиус – не математик и даже не опытный картограф – сумел составить свою карту.

Описание Райтом геометрической проблемы, связанной с новой проекцией, показывает ясность мышления и стиля. Он писал:

«Представьте сферическую поверхность с нанесенными на нее меридианами, параллелями и всей гидрографической информацией, вписанную в вогнутый цилиндр так, чтобы их оси совпали.

Пусть эта сферическая поверхность равномерно раздувается, как пузырь, пока не соединится с вогнутыми поверхностями цилиндра. Каждая параллель на этой сферической поверхности будет успешно расширяться от экватора к каждому полюсу, пока не станет одинакового диаметра с цилиндром, а меридианы будут расти, пока не окажутся на таком же расстоянии друг от друга, как на экваторе. Таким образом, проще всего понять, как сферическую поверхность можно преобразовать (расширением) в цилиндрическую, а потом и в поверхность параллелограмма»[130].

Конечно, этого было недостаточно для полного понимания того, что проблема упрощается, если цилиндр (который можно развернуть, образовав плоскую поверхность) использовать вместо сферы, однако это было больше, чем предполагали и Нуньес, и Меркатор. Было необходимо разработать новые таблицы, чтобы создавать карты на основе этой проекции. Райт это сделал. После публикации его труда любой картограф мог составить карту на основе уже ставшей знакомой проекции Меркатора, отлично приспособленной к морским картам – ведь теперь линия румба стала прямой, и постоянный курс по компасу можно было проложить, пользуясь линейкой. То, что курс по дуге большого круга не так прост, очевидно, все еще не заботило моряков, не заинтересованных в нахождении кратчайшего расстояния между двумя точками, поскольку ветры и течения все равно не позволят им пройти точно этим курсом.

Новая проекция не стала тотчас популярной, хотя для следующего поколения уже была вполне привычной. Если она не распространилась быстрее, то лишь потому, что карты были чрезвычайно популярны и, даже не слишком качественные, хорошо продавались. Многие карты предназначались не для моряков, а для джентльменов, «чтобы украсить их залы, гостиные или библиотеки» – это отметил Джон Ди в примечании к Евклиду. Моряки отдавали предпочтение «Маринерс Миррор» (1583). Это было простое и удобное пособие, содержащее элементарные навигационные методы, таблицы, астрономические правила и старомодные карты европейских вод. Издатели, неоднократно перепечатывавшие его, не видели никаких оснований для усовершенствования книги, даже когда появились лучшие карты. Оно все равно пользовалось спросом.

В 1605 году Генеральные штаты (парламент) Нидерландов поручили Виллему Блау (1571–1638) написать новое пособие для судоводителей. Блау принадлежал к научной школе картографов: он был не только издателем карт, но также компетентным и опытным изготовителем измерительных инструментов. Два года он провел у Тихо Браге в Ураниборге, изучая астрономию, географию и устройство точных инструментов. Результатом его работы стала книга «Свет навигации» (The Light of Navigation, 1612) – хорошее пособие, снабженное исправленными астрономическими и навигационными таблицами, а также новыми морскими картами в проекции Меркатора. Это была первая из многих работ, содержавших открытия конца XVI века. Теперь на первый план вышли английские математики, потеснив голландских и португальских. Лаг, бакстафф, разъяснение Райта меркаторской проекции – все это вошло в европейскую практику в первой половине XVII века.

Изготовитель инструментов был не единственным ремесленником, нуждавшимся в помощи математиков. Для инженеров математика тоже была важна. Гражданское и военное инженерное дело являлось востребованным и прибыльным занятием на всей территории Европы, и в первую очередь в Италии. В тот период был особенно велик интерес к машинам и механизмам, о чем свидетельствуют многочисленные книги с красочными иллюстрациями, в которых описывались силовые машины, насосы, мельницы, краны, военные машины, пневматические и гидравлические устройства и многое другое.

Здесь, конечно, тоже не обошлось без влияния гуманистов, но в основном интерес был вызван практическими технологиями, появившимися в конце XVI – начале XVII века, наподобие тех, что описаны в «Пиротехнике» (Pirotechnia) Бирингуччо или «Металлургии» (De Re Metallica) Агриколы. Практики, строившие всевозможные машины, разумеется, были знакомы с математикой, и появилось много изобретателей с математическим образованием, которые создавали приспособления для вырезания конусов, цилиндров и т. д. Рамелли (1531–1590) был убежден в преимуществах математических знаний, о чем не преминул поведать миру в предисловии к своей книге Le Diverse et Artificiose Machine (1588). Бессон называл себя «доктором математики», а машиностроение и инженерное дело – истинными целями математики. По его мнению, «машина – плод геометрии и, следовательно, ее цель»[131]. Это, конечно, идеализированное представление, но можно с уверенностью утверждать, что в XVI веке машиностроение считали математическим искусством.

Этой науке предшествовали механика и математическая физика: изучение, с одной стороны, законов простых и сложных механизмов, а с другой – состояние тел, на которых эти механизмы установлены, то есть статика и динамика. XV век не проявлял заметного интереса к таким проблемам. А в следующее столетие появился двойной стимул: опубликование средневековых трудов по физике, а также новое издание работ Архимеда. Трактаты Архимеда были хорошо известны средневековым ученым, но их подход к статике основывался не столько на методе Архимеда, сколько на псевдоаристотелевских «Механических проблемах». Это раннее теоретическое обсуждение теории простых механизмов воплощало динамический подход, рассматривая все случаи покоя как аналогичные равновесию весов[132]. Архимед, наоборот, занимался только покоем и считал статику частью математики. Его труды были слишком сложными, чтобы привлечь издателей XV века. Первый более или менее полный латинский текст (отрывки печатались и раньше) был версией, взятой из разных источников и плохо отредактированной, как утверждали его противники, Никколо Тарталья (1500–1557), и опубликованной в 1543 году. Более точный перевод с греческим текстом был опубликован годом позже[133].

Сочетание доступных текстов Архимеда и публикации средневековых трудов положило начало двум разным типам исследований. Интересные комментарии Леонардо да Винчи по статике явно уходят корнями в средневековые традиции. И наоборот: Симона Стевина в конце века мотивировали исключительно труды Архимеда и его статический подход и к проблемам равновесия, и к механике жидкости. Размышляя над старой проблемой, почему предметы на дне озера или моря не оказываются раздавленными весом воды, Стевин пришел к формулировке гидростатического парадокса – давление жидкости на погруженное в нее твердое тело пропорционально высоте столба воды над ним, а не всего объема жидкости, в которую оно погружено. Его логический квазиматематический подход был аналогичен позднее использованному Паскалем.

Стевин особенно гордился своим объяснением равновесного состояния тел на наклонной плоскости, которое он проиллюстрировал на титульной странице «Элементов искусства взвешивания» (The Elements of the Art of Weighing, 1586). Книга была опубликована на голландском языке[134]. Он представил себе треугольную поверхность АВС (рис. 6) с основанием АС, параллельным линии горизонта, а стороной АВ в два раза большей, чем сторона ВС. На поверхности он представлял бесконечную цепь, на которой через равные промежутки закреплено четырнадцать шаров одинакового размера и веса. Если нет вечного движения цепи по треугольнику, что Стевин считал абсурдным и невозможным, она должна находиться в состоянии покоя, причем два шара будут находиться на стороне ВС, а четыре – на стороне АВ. Иначе будет происходить вечное движение цепи по треугольнику. Поскольку цепь находится в равновесии, нижнюю часть можно убрать, не нарушая равновесия верхней. Отсюда длина наклонных плоскостей будет прямо пропорциональна весу тела, вернее, той его части, которая направлена вдоль плоскости. То же самое можно выразить другими словами: на наклонных плоскостях одинаковой высоты данная сила будет удерживать вес, пропорциональный длине плоскости. Обратите внимание, что Стевин использовал треугольник (хотя иногда он предпочитал называть его призмой). Он рассматривал вес как величину, аналогичную числу или размеру, и потому считал, что им можно оперировать как числом (арифметика) или размером (геометрия). Вместе с тем он не видел ничего особенного, выдвигая в этом математическом контексте аргументы против вечного движения как физической невозможности. Стевин по методам и воззрениям был последователем Архимеда, хотя и не таким строгим, как, например, ученик Коммандино Гвидобальдо дель Монте (1545–1607), чья «Механика» (1577) содержит скрупулезное развитие статических принципов.

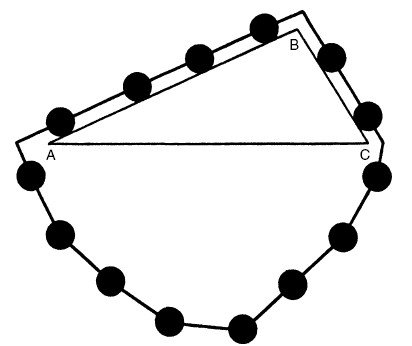
Рис. 6. Демонстрация равновесия на наклонной плоскости Стевина

Обсуждение Стевином условий равновесия тел на наклонной плоскости было интересным, оригинальным, но никоим образом не единственно возможным подходом к проблеме. Другой подход, основанный на изложенном материале в «Механических проблемах», использовал Йордан Неморарий в XIII веке. Эта традиция процветала одновременно с Архимедовой. На самом деле их можно было объединить, как это сделал Галилей (1564–1642) в трактате «О механике», который он написал в 1600 году для своих частных учеников в Падуе. Это элементарный анализ пяти простейших машин: наклонная плоскость, рычаг, ворот, шкив и шнек, с кратким описанием элементов, общих для всех. Хотя Галилей мало думал о вкладе в науку и не считал свои соображения сколь бы то ни было оригинальными, его труд был отмечен современными авторами. «Механику» читали в Италии (хотя до 1649 г. только в рукописи) и во Франции (в переводе Мерсенна).

Аристотелевские элементы, заметные в «О механике», никоим образом не означают, что Галилей в этот период был последователем Аристотеля, как бы глубоко ни увяз в перипатетической доктрине в молодости. Он стал противником Аристотеля и преданным учеником Архимеда, имя которого произносил с неизменным благоговением. Им уже был написан трактат «О движении» (De Motu, 1590), использовавший архимедову физику как оружие против динамических принципов Аристотеля. В этом подходе он находился под влиянием трудов Никколо Тартальи и Дж. Бенедетти. Многие авторы, писавшие о математике, – Леонардо да Винчи, Тарталья, Бенедетти и др. – уже пытались подвести математическую базу под теорию движущей силы. Эта теория, которую глубоко изучили в физике позднего Средневековья, возродилась к жизни в XVI веке, когда опыт канониров и набирающий силу антиперипатетический дух времени объединились, чтобы указать на ошибки, присущие аристотелевской теории о движении. Попытки ученых XVI века математизировать движущую силу были обречены на провал. Галилей это понял, завершив De Motu, потому что эта сила была качественной, а не количественной. Но сама невозможность попытки помогла Галилею понять необходимость в новой динамике, которая сумеет «примирить» разные подходы к движению тел.

Никто в XVI веке не мог писать о математике или физике движущихся тел, не отражая в той или иной степени идеи Аристотеля. Аристотель отнес все движение к среде, в которой движется тело, и также к его положению в пространстве. Любой, кто выступал против теорий Аристотеля – как, например, Бенедетти, – должен был помнить, что Аристотель удовлетворительно объяснил, как и почему тела падают, а метательные снаряды летают, и необходимо было придумать аналогичную теорию. «Естественное» движение, включая движение падающих тел, для Аристотеля не требовало другой причины, кроме предшествующего перемещения. Ведь естественное движение было результатом внутренней тенденции тела искать свое естественное место во Вселенной. Тяжелое тело стремится вниз – к центру – падает. Легкое тело, наоборот, стремится вверх. При этом «вниз» и «вверх» определялись относительно центра Вселенной. Абсолютно тяжелые и абсолютно легкие тела имели только одну тенденцию, относительно тяжелые и относительно легкие – это те, которые могли или подниматься, или падать, в зависимости от того, где находились. Смещенное тело «знает», что произошло, и, значит, «знает» свою цель, поэтому оно ускоряется при приближении к месту назначения.

В естественное движение вовлечен еще один фактор – среда. Признавая, что чем гуще среда, тем медленнее движение, Аристотель утверждает, что скорость обратно пропорциональна плотности среды. Поэтому в вакууме, где нет среды, скорость падающего тела будет бесконечной. Это было для Аристотеля показателем абсурдности и веским аргументом против существования вакуума. Опять же чем тяжелее тело, тем больше его способность преодолевать сопротивление среды и тем быстрее оно упадет, а значит, скорость падающего тела прямо пропорциональна его весу. Движение метательного снаряда, по соображениям Аристотеля, требует силы не только для того, чтобы инициировать движение, но и чтобы обеспечить его продолжение, потому что оно вынужденное, а не естественное. Для Аристотеля (как и позднее для Декарта) все такие движения должны проходить под воздействием, и он считал, что здесь тоже главную роль играет среда, придавая толчок вначале рукой или пращой. Но «подталкивание» среды постепенно уменьшается и в конце концов заканчивается. В этот момент тяжесть берет верх и тело падает. А поскольку вынужденное движение и естественное не смешиваются, считалось, что все метательные снаряды имели прямолинейную траекторию.

Теперь эти теории, хотя они, казалось, предлагали ответы на все вопросы, касающиеся тел в движении, были неудовлетворительными, их стали мало-помалу критиковать. Люди усомнились, действительно ли тела падают со скоростью, в точности пропорциональной их весу. Альтернативные варианты появлялись очень медленно, и только в самом конце классического периода комментаторы Аристотеля VI века сформулировали теорию импетуса. Эта теория сохранила общие очертания аристотелевской мысли, доктрины естественных мест и невозможности смешанных движений, но в то же время ее сторонники отвергли мнение Аристотеля о том, что тело продолжает двигаться после начального приложения силы, потому что его подталкивает воздух. Они сделали это по двум причинам: во-первых, воздух, как сказал Аристотель, сопротивляется движению, во-вторых, движение тяжелых тел продолжается дольше, чем легких, хотя воздуху двигать легкие тела легче. Эти логические заключения они подкрепили примерами из опыта, знакомыми фактами, которым предстояло повторяться еще много веков. Вместо теории Аристотеля они предположили, что движущая сила сообщает телу импетус, который становится качеством движущегося тела, как тепло является качеством горячего тела. В точности так же, как тепло исчезает, если убрать источник нагрева, и импетус исчезает, если убрать источник приложения силы.

Теория импетуса достигла своего расцвета в XIV веке. Английские и французские математики использовали ее, чтобы объяснить, почему падающее тело увеличивает скорость (потому что в каждый момент к процессу падения добавляется существующий импетус движения), обходясь без идеи, что скорость возрастает с приближением к цели. Импетус использовался даже для объяснения неизменного и вечного вращения небесных сфер. Ученые признали, что сама скорость (а не только импетус) могла рассматриваться как качество движущегося тела.

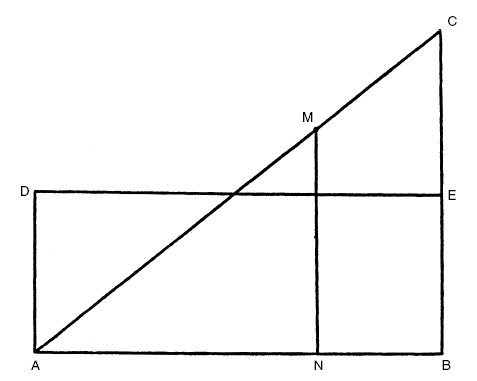
Рис. 7. Широта форм: геометрический анализ

Математикам пришлось изрядно потрудиться, чтобы вывести геометрические и арифметические выражения для изменения качеств в общем. При этом они исходили из допущения, что «интенсивность» любого качества (тепло, белизна) может быть обозначена численно. Так тело с теплом 8 будет горячее, чем с теплом 4, а скорость 8 будет больше, чем скорость 4. (Разумеется, эти числа произвольны и не имеют физического смысла.) Один из важных вопросов – сравнение качества, которое изменяется (скажем, от 9 до 1), с качеством, остающимся неизменным, – процесс получил название «исчисление (calculus) качеств». Самым любопытным представляется такое исчисление для обсуждения «широты» или вариации форм и качеств, разработанное Николаем Орезмом (Оремом), великим математиком и философом XIV века, работавшим в Парижском университете. По сути, это метод изображения «интенсивности» качества – графическое представление переменной величины в зависимости от времени (или, скажем, пространственных координат). Если изменение линейное, Орезм называл его униформным, если нелинейное – дифформным. Таким образом, он представлял униформное изменение наклонной прямой, а дифформное – кривой. Так, на рис. 7 интенсивность любого униформно изменяющегося качества представлена длиной вертикальной линии MN. Она униформно возрастает по мере продвижения N от А к В.

Таким образом, на рисунке количество униформно изменяющегося качества MN есть площадь треугольника АВС, которая, в свою очередь, равна площади четырехугольника ABED, если Е – середина ВС. Отсюда Орезм делает вывод, что количество униформно изменяющегося качества такое же, как количество постоянного качества, эквивалентное среднему значению униформно изменяющегося качества.

Когда этот анализ был применен к движущимся телам, появилась необходимость рассматривать скорость как униформно изменяющееся качество – Орезм и другие ученые были к этому готовы. Из сказанного выше следует, что «количество» скорости, униформно изменяющееся от v до V, такое же, как «количество» постоянной скорости, что можно выразить равенством 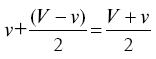. Единственная проблема – значение «количества» в этом случае: для Орезма оно значило, как предполагала его геометрия, расстояние.

Однако были и другие проблемы, которые не были решены, пока за них не взялся Галилей. Формула не применялась к падающим телам, поскольку не было достаточно смелых людей, чтобы предположить: падающие тела униформно ускоряются. Математики, которые обсуждали интенсивность и ослабление таких качеств, как скорость, не относили его напрямую к импетусу, который оставался полезным объяснением почему тело движется, не касаясь чисто математических аспектов.

Теория импетуса в XVI веке была весьма туманной и не имела последовательного развития. Ее использовали и для нападок на аристотелевскую теорию, и в стремлении понять действительные проблемы движущихся тел. А молчаливая вера в то, что теория импетуса может рассматриваться в Архимедовом духе (что невозможно), неизбежно вела к путанице. Кроме того, каждый математик интересовался каким-то одним аспектом проблемы и почти никто не изучал кинематику в целом. Так, Тарталья занимался движением тел, почти исключительно с точки зрения баллистики, и его задача отнюдь не облегчалась попыткой примирить аристотелевскую физику с наблюдениями канониров. (Несмотря на то что кажется очевидным, на самом деле речь шла вовсе не о примирении традиционной и устаревшей теории с открытиями проницательной эмпирики; канониры делали не меньше ошибок, чем Аристотель: они точно знали, что пушечное ядро, вылетев из дула, некоторое время увеличивает скорость, так что дульная скорость не является максимальной.) Тарталья считал придание импетуса ответственным за вынужденное движение, но долгое время верил, как и Аристотель, что естественное и вынужденное движение не могут смешиваться. Поэтому траектория снаряда должна состоять из двух прямых линий. Впоследствии, возможно на основании наблюдений, он решил, что сила тяжести действует постоянно и всегда отклоняет снаряд в сторону от прямой, искривляя траекторию. Он сомневался, надо ли описывать ускорение падающего тела, исходя из его расстояния от начального пункта или до его конечного пункта, но так и не принял окончательного решения. Бенедетти, еще более ярый противник Аристотеля, чем Тарталья, наконец освободился от концепции «цели» и начал рассматривать только «прошлое» падающего тела, не пытаясь предсказать его «будущее» и желая только установить его скорость в любой данной точке.

Труд Галилея «О движении» (De Motu) выполнен в общих традициях Тартальи и Бенедетти. Хотя он намного превосходит их работы, но все же показывает, что даже такой проницательный ум, как Галилей, не мог передать проблему падающих тел и летящих снарядов ясно и просто, во всяком случае, пока она рассматривалась в рамках теории импетуса. Галилей написал элементарный, но исчерпывающий труд. В первых главах изложена природа тяжелого и легкого. Уже здесь он порывает с Аристотелем, отрицая существование легких тел. Легкость относительна. На самом деле все тела более или менее тяжелые. Представляется, что эту идею он вывел, размышляя о плавающих телах. И действительно, многое из этой части механики Галилея взято из гидростатики Архимеда. Вся его теория на этот счет может быть сведена к следующему утверждению: тела падают со скоростью, пропорциональной их плотности (а не их весу, как считал Аристотель), минуя плотность среды. Так что в воздухе, к примеру, тела, сделанные из одинакового материала, имеющего одинаковую плотность, будут падать с одинаковой скоростью, независимо от веса. Если есть два предмета с одинаковым весом, тот, что имеет большую плотность, будет падать быстрее. Если плотность – или плавучесть – среды будет постепенно уменьшаться, падение предметов успокоится постепенно, и в пределе (в вакууме) их скорость станет пропорциональна их плотностям. Так что, несмотря на заверения Аристотеля, движение в вакууме возможно, и предметы из разных материалов будут падать в нем с разной скоростью.

Используя вес как определяющий фактор, Галилей вывел несколько новых необычных идей относительно ускорения свободного падения. Согласно его объяснению, падающее тело должно сначала преодолеть силу, которая поместила его на место, значит, его начальное движение ускоренное. Когда достигнута характерная скорость падения, больше нет ускорения. Его и быть не может, утверждает Галилей, потому что постоянная сила порождает постоянную скорость. Поскольку тяжелым телам приходится преодолевать большую силу, они достигают характерной скорости медленнее, чем легкие. Тем самым Галилей отверг утверждение Аристотеля, что не встречающее сопротивления естественное движение будет бесконечно быстрым, как в вакууме, и открыл путь для дальнейшего рассмотрения скорости падающих тел без сопротивления среды. Одновременно Галилей был вынужден сделать вывод – истинная инерция невозможна, хотя он имел слабое представление о ее практическом существовании. После размышлений о наклонных плоскостях (на основании которых он позже пришел к заключению, что все-таки есть инерционное движение) он отметил, что, если взять идеально гладкое тело и поверхность с отсутствующей силой трения, можно сделать вывод, что тело на плоскости, параллельной линии горизонта, будет двигаться под воздействием очень малой силы, намного меньшей, чем любая данная сила[135]. Это очень близко к концепции инерции. Бенедетти сформулировал концепцию инерции более четко, но только применительно к абстрактным телам, двигающимся через геометрическое пространство.

Как Галилей сумел пройти долгий путь от физики Архимеда, Аристотеля и теории импетуса к совершенно новой динамике, неясно. Между De Motu и «Диалогом о двух главнейших системах» (1632) он очень мало писал о механике. После 1604 года в основном занимался астрономией и много времени уделял полемике. Но все же сохранились некоторые намеки на то, как он шел от одной системе к другой. Он хотел описать закон возникновения ускоренного движения при свободном падении. В письме Паоло Сарпи, датированном октябрем 1604 года, он писал:

«Я искал принцип, совершенно несомненный, который можно было принять за аксиому, чтобы описать следующее: расстояния, пройденные в естественном движении, относятся как квадраты времени, и, следовательно, расстояния, пройденные за равное время, относятся как серии нечетных чисел. А принцип следующий: тело, испытывающее естественное движение, увеличивает свою скорость в той же пропорции, что и расстояние до исходной точки».

И это самое любопытное! То, что доказал Галилей, является всем нам знакомым законом свободного падения, а именно s = 1/2 at2. Но естественный и очевидный принцип, на основании которого он вывел этот закон (мгновенная скорость пропорциональна пройденному расстоянию), совершенно неверен. То, что скорость связана с пройденным расстоянием, естественное предположение. Скорость, как полагали, была пропорциональна расстоянию (Леонардо, Бенедетти и впоследствии Декарт, который так и не сумел исправить эту ошибку). Это практически неизбежный результат попыток описать математически движение падающего тела. Ведь пока математикой считалась в основном геометрия, в первую очередь на ум приходило расстояние, а не время. Только намного позже Галилей пришел к пониманию того, что, хотя постоянная причина должна вызывать постоянное следствие, этим постоянным следствием может быть скорость изменения, а не фиксированная величина; иными словами, может быть неизменное ускорение, а не постоянная скорость. Отсюда в конечном итоге выводится закон инерции. Однако потребовалась более высокая в полном смысле этого слова степень математизации, прежде чем математическая точка зрения могла показаться по-настоящему совместимой с эмпирическим тестом, который Галилей, вероятно, уже проводил в это время, – скатыванием шаров по наклонной плоскости, как описано в «Беседах и математических доказательствах, касающихся двух новых отраслей науки» (Discourses on Two New Sciences, 1638). Тем не менее выводы 1604 года вполне подтвердили его веру в математический подход, хотя должны были еще пройти годы, прежде чем было выполнено математическое обоснование. Ранние труды Галилея показывают одновременно и силу и слабость прикладной математики XVI века в мире физических тел.

Данный текст является ознакомительным фрагментом.