Глава V. Лики Вселенной

Глава V. Лики Вселенной

Смелым искусством гордясь, свой мир приводя во вращенье,

Звездами высших небес правит умом, человек.

Клавдиан

Уныние и запустение царили там, где, как представлялось издалёка Марку Туллию Цицерону, квестору Сиракуз 76 года до нашей эры, божество забвения должно было с изумлением узреть непреодолимую для себя границу. Увы, здесь, на заброшенном кладбище некогда великих Сиракуз, можно было лишний раз убедиться, как быстро забывают смертные о деяниях даже самых великих сынов своих. Вот уже битый час Цицерон отыскивал гробницу, с трудом пробираясь через колючие заросли дикого кустарника. Он уже начал терять надежду найти памятный камень, достойный коленопреклонения каждого, понимающего в науках. Желая побыть у могилы в одиночестве, квестор отклонил предложение взять провожатого и теперь раскаялся в этом. Имя того, кто почти полтора века назад был с горестными плачами погребен под одним из этих безымянных могильных холмов, поросших крапивой, зловещей травой забвения, Цицерон впервые услышал много лет назад от Посидония из Апамеи. Тогда, в лета зеленой юности, отправился он на остров Родос в надежде набраться знаний в школе философов, знаменитой в те времена во всем Средиземноморье. Посидо-ний, выдающийся историк и географ, друг Перикла, глава этой школы, стал для неофита кладезем премудрости. Его осведомленность в науках была поразительна, и Цицерону, узнававшему с того времени немало от других учителей, от друзей, а также и из книг, порой казалось, что обо всем этом он уже слышал некогда из уст Посидония, премудрого и терпеливого наставника юношей.

Но ничто из услышанного от учителя не производило на него такого впечатления, как повествования философа о небесной науке. И тогда уже Цицерона удивляло одно странное обстоятельство: Посидоний, рассказывая о том, что именно шаг за шагом узнавали о Вселенной его предшественники, будто и не замечал вопиющего противоречия: по его словам получалось, что великие мудрецы назойливо открывали смертным глаза на одно и то же, то ли не зная достигнутого предшественниками, то ли забывая об этом, то ли (неужто и они подвержены низменным человеческим страстям?) преднамеренно замалчивая успехи своих учителей, словно желая придать себе славы. Или, может быть, Учитель просто не хотел обделить никого из почтенных мудрецов и потому щедро воскуривал фемиам каждому из «семи самых достойных»?

Вот хотя бы великий Фалес. Выходило так, что он уже полтысячелетия назад знал продолжительность лунного месяца и солнечного года, изобрел гномон и солнечные часы и с помощью их, сопоставляя размеры тени в разное время года, осведомил греков о странах света, о равноденствиях и солнцестояниях и даже неодинаковой продолжительности сезонов года. Ведомы ему были и клепсидры, водные часы. Посидоний утверждал даже, что Фалес сумел однажды, окончательно сразив эллинов своим всеведением, определить, когда «день превратится в ночь». Предсказание сбылось в урочное время — утром 28 мая 585 года до нашей эры, когда на пограничной реке Галюс сошлись готовые к бою войска мидян и лидийцев, возглавляемые Алпаттой и Астиагоном, наступило полное солнечное затмение. Как частное (неполное) его наблюдали и сами афиняне, ошеломленные справедливостью предсказаний мудреца. Пройдет много лет, и завистливые к чужой славе станут утверждать, что Фалес воспользовался для предсказания этого ужасающего события вовсе не знанием сароса — календарного периода, когда затмения повторяются, а подсказками халдейских звездочетов. Другие вообще уверяли, что предсказать затмение можно без особых хлопот — стоит лишь заметить, что затмение светил всегда случается в пору, когда Луна в новолуние или полнолуние оказывается на одной и той же, шириной всего в полградуса, полоске Неба, по которой в течение года путешествует Солнце. Хорошо им было рассуждать об этом через пять веков после того затмения. Многое с тех пор познали астрономы!

Цицерон знал, что и в его время почитатели Фалеса, негодуя на недоверие к обширным познаниям мудреца, продолжают настойчиво уверять, что он, как и его великий современник Пифагор, знал «арктический круг», который невидимо определяет на севере границу той части небесного купола, звезды которой, обращаясь вкруг Полярной звезды, никогда не заходят за горизонт, а значит, и не умирают, символизируя вечность бытия в тех краях, куда на лунном серпе отбывают в должное время души умерших. Если он умел рассчитывать солнцестояния, то, продолжали стоять на своем почитатели, никого не должна удивлять осведомленность его о «летнем тропическом» и «зимнем тропическом» кругах, то есть об орбитах, по которым Солнце двигалось в Небе в дни летнего и зимнего солнцестояний. Между ними, посередине, как удалось установить ни кому иному, как Фалесу, размещался равноденственный круг — путь дневного светила в начале последней декады марта или сентября, когда сравнивались светлая и темная части суток. Разумеется, ведом ему был и «антарктический круг», который определял на юге границы видимых в Афинах звезд. Чтобы из-за него всплыли вдруг неизвестные афинянам звезды южной сферы Вселенной, следовало или дожидаться соответствующего тысячелетия, когда это могло произойти из-за покачивания в пространстве Земли, или (что проще) проплыть на корабле к северным берегам Африки и библейской земли. Как мореход-финикиец Фалес знал те звезды не понаслышке.

Умело он использовал и еще один круг, меридиан, который светила пересекали в положенное время в южной стороне, поднимаясь в этот миг над Землей на самую большую высоту. Меридиан, касаясь всех остальных кругов, совпадал на небосводе с линией, невидимо соединяющей север и юг. Поразительно, но Фалес, как уверял Посидоний, знал и так называемый наклонный круг — зодиак, «звездную дорогу» Солнца и Луны, которая касалась трех кругов — летнего и зимнего тропического, а также равноденственного. Путешествие по зодиаку «блуждающих звезд», планет, мудрец, кажется, не удосужился заметить, но в Вечерней и Утренней звезде справедливо усматривал одно и то же светило — Венеру.

Что же касается возможности предсказания затмения, то боготворящие Фалеса напоминали — он первым сказал о «темной землистой природе» Луны, о заимствовании ею света от Солнца, которое определяло и фазы ночного светила. И не ему ли принадлежит честь первым провозгласить истинный порядок размещения светил в глубинах Неба — Солнце достигало в своем движении «пределов мира», а Луна ближе иных небесных тел проплывала над Землей? Если же он додумался до всего этого, то как же можно всерьез сомневаться в том, что Фалес понимал истинную причину затмений и потому мог уяснить периодичность их? Недаром предания гласят, что он, объясняя неосведомленным солнечное затмение, прямо говорил о прохождении Луны перед Солнцем по прямой линии и об отражении ночного светила на огненном диске дневного, как в зеркале. Значит, с торжеством возглашали сторонники натурфилософа, Фалес, как и Пифагор, усматривая в Небе невидимые орбиты светил, зная порядок их размещения в пространстве и догадавшись об истинных причинах затмений, могли сделать вывод о том, что Земля шаровидна. Стоит ли поэтому сомневаться в том, что Фалес первым создал модель Вселенной со всеми ее кругами и сферами? Место их в пространстве мироздания определялось, по Фалесу, орбитами небесных светил, прежде всего Луны и Солнца, а циклы гармоничных движений их порождали время. Вот уж воистину справедливо говорил Фалес: «Мудрее всего время, ибо оно объясняет все», а значит, и устроение мира. Вторил ему и Гераклид Понтийский: «Бег времен. Солнце, блюститель и страж их, определяет, руководит, выявляет и открывает перемены и времена года, которые приносят с собою всё»:

Идея о том, что именно время определяло границы и структурные части мира, его костяк и облик в целом, стала, по-видимому, руководящей и для Эмпедокла, который писал о том, что границы мира определяют круговые движения Солнца. Оно же очерчивало и в целом контур его, напоминающий лежащее яйцо. Недаром расстояние от шаровидной Земли до Неба, в зените считалось натурфилософами меньшим, чем протяженность мира по ширине. Как объяснял Эмпедокл, это потому, что Солнце, сжимая воздух, отклонило полюса, из-за чего север поднялся, а юг опустился.

Вот сколь многое знал Фалес, и как же можно продолжать сомневаться в том, что он мог предсказать затмение? — возмущались обожатели первого мудреца греков. Странно было бы знать все сущее о мироздании и растеряться перед решением простой задачи. Но Цицерон был осведомлен о главной сложности утверждения Фалеса на тропе мудрейшего. Века не пощадили трудов философа, и сведения о его достижениях хранились большей частью в устных преданиях. А они ведь разные бывают, эти вольные людские повествования. Посидоний по такому случаю рассказывал обычно притчу, которая по замыслам завистников Фалеса должна была продемонстрировать его невежество, очевидное даже простолюдинам: «Однажды, выходя из дома наблюдать звезды в сопровождении прекрасной насмешливой фракиянки, Фалес, сын Эксамия и Клеобулины финикийского рода Фелидов, самого знатного во всем потомстве Кадма, восторженно глядя вверх, молвил: "Как прекрасно подмечать все небесное!" И случилось так, что мудрец при этих словах свалился в колодец. Фракиянка помогла звездочету выбраться из западни и сказала: "Стараясь постигнуть небесное, ты не замечаешь того, что под ногами"». Посидоний, посмеиваясь, тут же развенчивал притчу, иначе толкуя причину смеха красавицы. Дело, надо думать, было совсем не в издевке над ничтожностью познаний Фалеса в неземной науке. Красавица досадовала, что отрешенный от мира сего философ не замечает истинно красивое под боком у себя, а ищет его на недоступных высях.

Посидоний призывал учеников доверять иным сведениям, положим, повествованию Апулея о том, что Фалес, когда возраст его приближался к 80 годам, определил диаметр Солнца и рассчитал, что это составляет 1/720 его звездного пути в течение года. Вот каких тонкостей достиг он в познании светил! Сам изумленный своим достижением, Фалес по преданиям тотчас сообщил о том Менандру Приененскому. Тот пришел в восторг от такого неожиданного знания и спросил, какую награду желает получить мудрец за свое открытие? Фалес, немало, надо думать, повидавший на своем веку при общении с философами, ответствовал весьма примечательно: «Для меня будет достаточной наградой, если того, чему ты от меня научился, когда станешь сообщать это другим, не припишешь себе, но объявишь, что это открытие принадлежит мне более, чем кому-нибудь другому».

Посидоний, повествуя об этом, намекал ученикам на причину замалчивания открытий Фалеса его недоброжелателями. Они, тайно заимствуя познанное им, его же во славу свою и срамили, обвиняя великого мудреца в невежестве. Теперь, когда в далекое далеко отошли времена Фалеса, иные философы, современники Посидония, с трудом разбираясь в тайнах мироздания, усомнились в том, что он смог познать их в столь давние времена. Они решили, что Фалес, наверное, многое выспросил у египетских или халдейских жрецов, а затем без зазрения совести выдал соотечественникам за свои открытия. Обманщик он, а не мудрец!

Как мог понять Цицерон из долгих бесед с Посидонием, среди ученых греков находились и такие, кто предпочитал отдать пальму первенства в открытии небесных премудростей Анаксимандру. Это он, великий натурфилософ первой половины VI века до нашей эры, надоумил будто бы спартанцев использовать гномон и солнечные часы, установил, что Луна заимствует свой свет от Солнца, открыл равноденствия и солнцестояния, положил начало познанию зодиака, вычислил наклон как солнечной, так и лунной «дороги» по отношению к небесному экватору. Люди неосведомленные твердят, что будто бы Клеострат Тенедосский сподобился открыть знаки зодиака (и прежде всего Овна и Стрельца) во второй половине VI века до нашей эры. Это произошло раньше, и слава открытия принадлежит Анаксимандру. Недаром же рассказывают предание, по которому именно ему принадлежит честь создания первой модели Земли. Есть люди, уверяющие, что он даже пытался устроить «изображение Неба». Значит, Анаксимандр конструировал модель всего мира.

А раз так, то, конечно, он ранее, чем кто-либо из эллинов, стал различать недвижные звезды и блуждающие планеты, определил порядок размещения светил в пространстве, орбиту Солнца считал в 27, а Луны — в 19 раз больше Земли, а понимая причину затмений и наблюдая начало их, пришел к выводу о равенстве размеров Солнца и Земли. Анаксимандр раздумывал о размерах Земли и вычислил, что толщина земного диска составляет 1/3 его горизонтального диаметра. Он высказал мнение, что некогда небесный свод вращался горизонтально, то есть полюс совпадал с зенитом, и только позже, когда на Земле появились живые существа, ось мира склонилась к северу, чтобы заселенными оказались лишь те зоны, где климат был особо благоприятным.

Анаксимандр велик и тем, что воспитал достойного ученика — Анаксимена Милетского. Но странно, разводил руками Посидоний, есть сочинения, в которых уверяется, что это он и никто другой изобрел гномон и установил в Лакедемоне сциотерион, солнечные часы. Находятся такие, кто именно ему отдает предпочтение в вопросе о том, кто первым в Элладе заметил планеты, «движущиеся звезды». Это он, оказывается, разгадал, рассуждая о «темных телах», причину затмений, смело объявил соотечественникам, что Луна заимствует свой свет от Солнца, толково объяснил механику смены ее фаз, расставил на должном расстоянии от Земли небесные светила. Последователи Анаксимена и слушать не хотели, когда поклонники Анаксагора из Клазомен пытались втолковать им, что этот великий мудрец в V веке до нашей эры первым объявил о Луне как о теле непрозрачном, но отражающем свет Солнца, понимание чего, видите ли, и позволило ему осчастливить греков знанием как причин регулярности смены фаз ночного светила, так и внезапного затмения то Луны, то Солнца. Итак, Анаксагор, выходит, перестал довольствоваться тем немногим из познанного Гомером и Гесиодом в мифологические времена эллинской истории.

Но великими представляются и достижения в астрономии младшего современника Анаксагора — Энопида Хиосского. У него тоже находятся почитатели, которые приписывают ему открытие «опоясания» и «косого положения» зодиака, установление наклонов орбит планет, определение 12 знаков зодиака. Энопид сподобился первым заметить, что в течение ночи над горизонтом появляются пять следующих друг за другом созвездий, начиная с противоположного Солнцу, которое восходит с заходом светила, и кончая последним, предваряющим восход его.

У Анаксагора, впрочем, как отмечал Посидоний, было одно слабое место в объяснении поведения двух главных светил Неба, что неизменно и порождало язвительные насмешки пифагорейцев. Он не воспринимал движение Солнца и Луны меж звезд по небесному кругу, зодиаку, а считал, что светила эти, совершая круговороты вокруг Земли, то сдвигались на север, то возвращались обратно на юг, перемещаясь по линии, перпендикулярной экватору. Движение Солнца и Луны в таком направлении приводил, по его мнению, сжимаемый ими холодный воздух, который, размягчаясь, согреваясь и уплотняясь, как пружина, отталкивал их в определенный момент назад. Этот момент как раз и совпадал, учил мудрец, с солнцеворотами. Анаксагор, не задумываясь над аргументами пифагорейцев, опрометчиво считал случайным возвращение Солнца через год, а Луны через месяц к тому же летнему или зимнему тропическому кругу и к соответствующим созвездиям. Случайным выглядело в его главах и путешествие светил, в том числе планет, в пределах одной и той же небесной дороги. В действительности же, как учили пифагорейцы (и на том настаивал Посидоний), это было следствие их собственного движения с запада на восток по кругу среди зодиакальных созвездий в направлении, противоположном суточному круговому движению с востока на запад. Поклонники Анаксагора в пику пифагорейцам всячески подчеркивали, что это он, а не их Учитель первым разъяснил причину затмений, а это ведь, как говорится, тоже не безделка: «Затмения Луны происходят от того, что ее загораживает от Солнца Земля; солнечные же затмения бывают, когда во время новолуния Луна загораживает собою Солнце».

Нелегко было Цицерону воспринимать толкования Посидония, о небесной науке. А Учитель к тому же предостерегал, что посвятить себя всецело премудростям ее небезопасно. Знания такие настораживают профанов, коим всюду мерещится ниспровержение основ, сиречь — богоотступничество. Уверенные, что натурфилософы только морочат головы людям, ревнители божественных устоев мира не прочь отправить их в «добровольное» изгнание, а то и решить спор об истине поубедительнее — заключить инакомыслящего в тюрьму, казнить или принудить «добровольно» принять яд. Стоит ли поэтому удивляться, что Сократ, которого сходные обстоятельства впоследствии вынудили отравиться, однажды, удрученный бестолковщиной собеседника, изрек в отчаянии: «Астрономия недоступна человеческому пониманию, и потому заниматься ею неразумно».

Посидоний умел, однако, довести до неофита свое понимание устройства мироздания и гармонии его «жизни» — цикличных перемещений светил по небесному куполу. Беседы по астрономии завершались демонстрацией созданной его руками «сферы» — механической модели Вселенной. Она приводилась в движение, и любой зрячий мог видать — «каждый ее оборот для Солнца, Луны и пяти блуждающих звезд то же, что происходило в Небе в любой день и любую ночь». Ученики знали скромность Учителя — он вовсе не представлял дело так, будто первым сотворил подобие всего мира. Посидоний отдавал пальму первенства в появлении такой идеи Платону, который однажды предложил своему любимому ученику Евдоксу Книдскому рассчитать геометрическую модель мироздания. Будущий выдающийся математик, медик, астроном, оратор, философ и географ, получивший достойное его деяниям прозвание — «Знаменитый», воссоздал мир из 27 гомоцентрических сфер. Они равномерно вращались вокруг шаровидной Земли, ибо к тому времени идея Фалеса, Пифагора, и Парменида из Элеи о том, что Земля круглая, перестала подвергаться ожесточенным нападкам и воспринималась натурфилософами спокойно.

Модель Евдокса давала не просто, как у Эмпедокла, самое общее представление относительно особенностей движения Солнца, Луны и планет и их местонахождения в пространстве. Конкретные количественные характеристики вращения их создавали предпосылки сооружения искусственной сферы, которая могла чисто механически воспроизводить перемещение небесных тел. Задача такая ко времени Платона и Сократа представлялась исполнимой, ибо за 200 лет после Фалеса греки узнали поразительно много: помимо путей движения Солнца и Луны, число планет, закономерности их перемещения по Небу, в том числе время оборотов, периоды остановок и попятного хода. Как величайшее достижение Евдокса Книдского Посидоний оценивал разработку им первой в истории греческой астрономии теории затмений. Ему он отдавал пальму первенства в установлении продолжительности периода повтора их, знаменитого сароса, включающего в себя 223 синодических месяца, равных, как он исчислил, 242 драконическим месяцам, что составляло 18 солнечных лет+11 дней, равных, оказывается, 19 драконическим годам. Посидоний не утаивал от учеников, что далеко не все натурфилософы верили, что эта задача оказалась по плечу Евдоксу. Скептики, учитывая ее головоломную сложность, упрекали Евдокса в том, что он утаил заимствование сароса все у тех же всезнающих халдейских жрецов.

Очередной вариант модели мира из 34 сфер создал Калипп из Кизика, ученик Аристотеля и астронома Полемарха, того самого, кто познавал законы Неба у Евдокса Книдского. Посидоний представлял Калиппа как астронома, которому удалось с точностью до суток определить продолжительность времен года: весны — 94, лета — 92, осени — 89, зимы — 90 суток. Это, по его мнению, было ближе к истине, чем определение длительности тех же календарных периодов современником Метона Эвктемоном, известного наблюдением в Афинах затмения Солнца 27 мая 432 года до нашей эры (соответственно 93, 92, 89, 89 суток).

Посидоний с увлечением рассказывал и о других достижениях греков в астрономии. Так, Гераклит Понтийский, размышляя над изменениями блеска планет, пришел к выводу, что они движутся вокруг Солнца, а не Земли, и не по круговым, а по эллиптическим орбитам. Автолик из Питаны усердно занимался уточнением времени восхода и захода Солнца во время смены сезонов, наблюдал восходы и заходы зодиакальных звезд, а также тех, что находились вне пояса зодиака. Гиппарх добился еще большей точности в определении длительности сезонов при той же последовательности их смен — 94 1/2, 92 1/2, 88 1/8, 90 1/8 суток. В итоге полугодие между осенним и весенним равноденствиями, которое оказалось по его расчетам равным 178 1/4 суткам, почти не отличалось от принятого в Вавилоне.

Что касается затмений, то изумление учеников, слушающих Посидония, вызвало создание Апполонием Пергским за два века до нашей эры таблиц, отражающих закономерности движения Луны. Это небесное светило он изучал столь дотошно, что заслужил прозвище «Эпсилон»— по названию знака, напоминающего по виду серп. Таблицы Апполония, наставлял Посидоний, позволяли рассчитывать позиции Солнца и Луны на небосводе в момент затмения. Речь, в сущности, шла, насколько мог понять Цицерон, о выделении неких циклично повторяющихся календарных периодов, когда эти светила и Земля занимали в пространстве то положение, когда можно было ожидать затмения Луны или Солнца.

Особая тема бесед на Родосе — о преувлекательнейшем деле, коим астрономы занимаются вот уже несколько веков — исчислении так называемых гелиаков, временных циклов, по истечении которых светила возвращались в некое исходное положение. Это был поиск общего кратного времени обращения их в пределах небесного купола. С именем знаменитого реформатора Солона или Клеострата Тенедосского Посидоний связывал установление восьмилетнего цикла счисления времени. Этот период, растолковывал он, был удобен тем, что целое число солнечных лет в нем с удовлетворительной точностью соответствовало целому числу синодических месяцев — 99, что и позволяло, считая время по лунным годам, выравнивать течение его по Солнцу не по произволу должностных лиц, а на основании точных астрономических наблюдений. Ученикам школы приходилось осваивать также суть гелиаков Метона (19 лет), Филолая и Энопида Хиосского (59), Калиппа (76), Демокрита (82), Евдокса, Арпала и Эратосфена (160 лет), Гиппарха (304 года + 1 сутки), Аристарха Самосского (2484) и побившего всякие рекорды Гераклита (10800 или даже 36 тысяч лет). Образ Вселенной Гераклит, однако, воспринимал традиционно — как громадный животный организм.

Шедевром считал Посидоний «небесный глобус», созданный сыном астронома Фидия, математиком, астрономом и механиком Архимедом. Его модель «подобия мира в выпуклой округлости меди» представляла собой сплошное тело, «одну неразличимую массу» со множеством «колес», «сочленений», «выходов для голоса» и «армией флейт». Это была гидравлическая машина, которая «воспроизводила небесные вращения» и «каждодневные неравные движения» светил, в том числе «различные течения» планет и зодиакальных созвездий. На шаре из меди при несходных движениях во время одного оборота демонстрировался восход и заход Солнца, рост и убывание Луны, причем Луна сменяла Солнце в течение стольких же оборотов, во сколько дней она сменяла его на самом Небе, вследствие чего и на небесной сфере происходило такое же затмение Солнца, а Луна вступала в ту же мету, где была тень Земли.

Прошли годы, и Цицерон однажды удостоился чести лицезреть в Риме чудо, сотворенное умом и руками «пленника муз» Архимеда. Две изготовленные им модели Вселенной вывез из Сиракуз полководец Марк Клавдий Марцелл («в то же время не доставив оттуда в свой дом ни одного другого предмета из столь значительной добычи»). Одну из сфер он оставил себе, а другую пожертвовал в храм Доблести, построенный им за Копенскими воротами столицы по обету, данному перед сражением под Кластидием в 222 году до нашей эры. Увидев небесный глобус Архимеда в действии, Цицерон понял, что Посидоний нисколько не переусердствовал в похвалах создателю медной сферы. Потрясенный Цицерон решил, что сицилиец обладал дарованием большим, чем то, каким может обладать человек. Ему подумалось: «Если кто-нибудь принесет в Скифию или Британию такую сферу, то кто в этих варварских странах усомнится, что ее создал разум? А вот относительно мира, откуда все проистекает, рождается, они сомневаются, возник ли он случайно или же благодаря божественному расчету и разуму. И они думают, что более велик Архимед, который создал подобие вращающейся сферы, чем природа в своем творении. Особенно важно, что во многих отношениях само творение искуснее своего подобия. В самом деле, когда Архимед заключил в один шар все движения Солнца, Луны и пяти планет, то он совершил то же, что и платоновский бог, творец мира в "Тимее"».

…Цицерон все-таки нашел место, где был похоронен убитый воином Марка Клавдия Марцелла великий Архимед, и преклонил колена перед прахом его. В последние часы жизни, как писал Тит Ливий, он «среди дикого смятения, под крики и топот озверевших солдат спокойно размышлял, рассматривая начерченные на песке фигуры. Грабитель заколол его мечом, даже не подозревая, кто это». На поверхности поваленного надгробия едва просматривались изображение шара, вписанного в цилиндр, и формула соотношения их объемов и площадей. Да, это он похоронен здесь — доказательство соизмеримости шара и цилиндра Архимед считал своим величайшим достижением, потому и завещал начертить эти фигуры на памятной стеле…

Потомки же рассудят иначе. Главным достижением Архимеда они назовут воссозданную в металле механическую модель Вселенной. Недаром она и полтысячелетия спустя вдохновила Клавдиана восславить торжественными строками волшебно-певучего гекзаметра безграничное могущество человеческого разума:

Неба устав, законы богов, гармонию мира —

Все Сиракузский старик мудро на землю принес.

Воздух, сокрытый внутри, различные движет светила

Точно по дивным путям, сделав творенья живым.

Ложный бежит зодиак, назначенный ход выполняя,

Лик поддельной Луны вновь каждый месяц идет…

Никто и сейчас не усомнится в величии Архимеда, а равно в величии Фалеса, Анаксагора, Анаксимандра и других мудрецов эпохи античности. Отчего же до сих пор продолжаются ожесточенные споры о приоритетах признанных прародителей греческой науки, о превосходстве в этой области то ли Востока над Западом, то ли Запада над Востоком? Головоломная путаница и странные неопределенности тут столь велики и очевидны, что, кажется, нет надежды разрешить противоречие. Да ведь не может быть и того, что на протяжении каких-нибудь 300–400 лет древнегреческие натурфилософы многократно с нуля накапливали астрономические знания, каждый раз поражая своих современников великими открытиями!

А что если безнадежность отыскания истины в таком вопросе — результат не слабости человеческой памяти или соперничества античных мудрецов, как я рискнул представить? При более осторожных размышлениях обо всем этом археолога палеолита (то есть в проблемах античности — «человека со стороны») тупиковая ситуация видится порождением двух обстоятельств: противоречивостью скудных сведении, по которым историки пауки воссоздают картину накопления естественно-научных знаний в культурах Средиземноморья и Ближнего Востока, и традиционным недопущением мысли, что многое из того, в чем будто бы один за другим прозревали античные натурфилософы, тысячелетиями ранее знали их безымянные предшественники, которые бережно сохраняли и передавали от поколения к поколению расшифровки сокровенных тайн Неба, и так продолжалось вплоть до времен Гомера и Ромула, Гесиода и Фалеса, Пифагора и Анаксимена.

Речь идет о безвестных мудрецах древнекаменного века. Имена их никогда не узнают люди, сколь бы изощренный поиск они ни вели, ибо могилы их забыты навеки…

…Снова ведут вверх, на третий этаж Эрмитажа, знакомые ступеньки спиральной лестницы. Но теперь там должна состояться встреча с иным «предметом искусства» из прибайкальской Мальты, найденным М. М. Герасимовым в то же, необычайно счастливое для него лето 1929 года. Археологи, склонные усматривать в объектах древних культур что-нибудь знакомое, сначала нарекли это изделие из бивня мамонта, которое лежало среди развалин жилища, пряжкой, потом стали называть ее бляхой, решив: если она для чего и могла сгодиться, то разве для украшения одежды дикаря. Резон здесь как будто был: выпуклую сторону подпрямоугольной пластины слоновой кости покрывали спиральные, в виде извивающихся змей, узоры, составленные из многих сотен лунок, вогнутую — резные изображения кобр, а в центре располагалось сквозное отверстие (трудно, правда, сообразить, как можно использовать пряжку с одной дыркой!). И вот нашелся фантазер, немецкий искусствовед и мифолог Карл Хентце, который усмотрел в змеевидных спиралях мальтинской пластины символы эволюций фаз Луны и даже иносказательные картины всего космоса! Другие пробовали считать лунки, пытаясь разглядеть в них календарные знаки. Никто из уважаемых палеолитоведов не воспринял тогда эти идеи всерьез. Однако результаты расшифровки знаковых систем ачинской скульптуры из бивня мамонта и украшений из погребения ребенка в Мальте позволили заподозрить неладное в однозначном решении такого вопроса. Спиральные луночные узоры на пластине это подозрение усиливали…

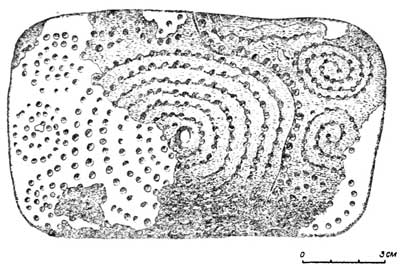
Пластина из бивня мамонта с узорами из лунок (выпуклая сторона).

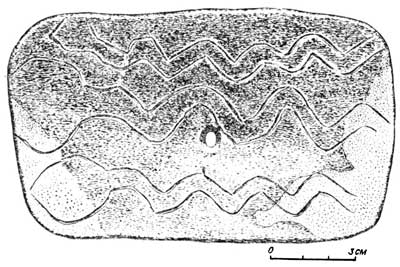
Оборотная (вогнутая) сторона той же пластины с изображениями змей.

Проверка орнамента «бляхи» на предмет выявления семантически значимой записи требовала точности абсолютной. Вот почему на сей раз по спиральной лестнице поднимался вместе со мной и художником Вячеславом Иосифовичем Жалковским кандидат архитектуры Виктор Иванович Сазонов. Он нес в портфеле специально для этого случая сконструированные приспособления, позволяющие с точностью до долей миллиметра определять в проекции позицию каждого знака пластины и их очертания по контуру. В течение недели орнамент был скопирован и настала пора приступить к самому волнующему: проигрышу вариантов «прочтения» текста луночной записи, сделанной 24 тысячи лет назад.

При проведении этого исследования прежде всего необходимо было четко уяснить, что предопределяло выбор художником древнекаменного века Сибири видов узора (спиральность, месяцевидность, змеевидную волнистость), а также отбор совершенно определенного количества лунок, составляющих пунктир орнаментальных структур мальтинской пластины, затем подтвердить их числовую значимость и тем самым положить конец разговорам о небрежном восстановлении М. М. Герасимовым знаковой системы левой части изделия (когда его извлекли из глины, то хорошо заметные лунки левого отдела из-за плохой сохранности поверхности пришлось специальным образом закреплять).

Орнаментальная композиция пластины с ее семью структурами. Числа, размещенные рядом с каждой из них, обозначают количество лунок.

Вопрос о качестве реставрации приобретал при расшифровке принципиальное значение, поскольку речь шла о правомерности использования «пряжки» в особо важных реконструкциях из области духовной культуры древнейших обитателей Сибири. Иначе говоря, ставилась задача лишить основания попытки компрометации этой уникальной находки М. М. Герасимова как открытия, по словам К. Хентце, «фундаментального для исторической науки». Единственным неотразимым доводом в таком предприятии могла стать лишь бесспорная (и притом, по возможности, не тривиальная), календарная значимость количества лунок в каждой из восстановленных М. М. Герасимовым орнаментальных структур левой части мальтинской пластины, о чем он при реконструкции, разумеется, не подозревал и потому заниматься «подгонкой» не мог. Тот же довод сохранил бы, естественно, силу и при отклонении суждений о случайностях числовых совпадений.

Совпадения между тем не замедлили появиться сразу же: как выяснилось в ходе изучения орнамента пластины, ее узор составляли семь структурных частей — число знакомое по лентам спиралей ачинской скульптуры и подвескам ожерелья из мальтин-ского погребения. Орнаментальную композицию составляли следующие элементы.

Центральная спираль. Она одинарная, разомкнутая, с отогнутым концом внешнего витка или обвода; ее знаковая система оказалась не столь простой, как ее представляли ранее: 242 лунки были связаны с семью резными концентрическими витками (они или «прислонены» к криволинейной резной линии, или как бы «нанизаны» на нее); лунка р располагалась за пределами резной линии внешнего витка спирали, в районе ее отогнутого конца и сквозное отверстие а — в центре спирали. Поэтому знаковую систему центральной спирали мальтинской пластины можно представить следующим образом:

242 + 1р + 1а.

Выведенная за пределы резной линии лунка р и совершенно особый знак — сквозное отверстие а — были призваны, как можно догадываться, представлять варианты количества счетных знаков центральной спирали, отличающиеся друг от друга всего лишь на 1–2 единицы:

242 ? 242 + 1 = 243 ? 242 + 1 + 1 = 244.

Периферийные спирали и месяцевидная фигура, расположенные слева от центральной спирали:

двойная, замкнутая, с противоположной закруткой витков спираль нижней части левого отдела пластины. Из-за того, что лунка с в этой спирали двойная, ее знаковая система может быть представлена в двух числовых вариантах, отличающихся друг от друга на единицу: или 62 (при подсчете лунка с воспринимается как знак 1), или 63 (учитываются оба отдела лунки);

двойная, замкнутая, с противоположной закруткой витков спираль верхней части левого отдела пластины — ее составляют 45 лунок;

месяцевидная фигура слева вверху. 14 лунок, составляющих ее, отчетливо подразделяются на два блока: серповидный или лодковидный полукруг — десять лунок и размещенные в пределах серповидного полукруга четыре лунки. Знаковую систему месяце-видной фигуры можно представить в виде следующей цифровой записи:

10 + 4=14.

Периферийные спирали и змеевидная линия, расположенные справа от центральной спирали: двойная, замкнутая, с противоположной закруткой витков спираль нижней части правого отдела пластины. В ее знаковую систему входят: 57 лунок, связанных с резными концентрическими витками верхнего отдела спирали и рассредоточенные концентрически без резных витков в нижнем отделе, и лунка о, выведенная за пределы резной линии внешнего витка верхнего отдела спирали. Знаковую систему двойной спирали нижнего правого отдела пластины можно представить в качестве следующей цифровой записи:

57 + 1;

одинарная, с отогнутым концом спираль верхней части правого отдела пластины; ее знаковую систему составляют 54 лунки;

змеевидная линия из 11 лунок в верхней части. В ее знаковую систему входят: четыре лунки, связанные с правым концом линии; пять лунок, связанных с ее левым концом, две лупки центрального отдела линии (они «прислонены» снизу к резной змеевидной линии). К этим лункам снизу примыкают, как бы акцентируя на них внимание, короткие зигзагообразные резные черточки л и м, поэтому и лунки эти определим теми же литерами. Знаковую систему змеевидной линии можно представить следующим образом:

4 + 2 + 5 = 11.

Общее число знаков на пластине (максимальное, при условии, что двойная лунка с в спирали левой периферии пластины соответствует двум знакам) составляет 489:

244+ [63 + 45+ 14]+ [58+ 54+ 11]=489.

При том же условии количество знаков в центральной спирали оказывается близким числу их во всех периферийных структурах орнамента пластины вместе взятых:

242 + 1 + 1 = 244,

[63 + 45 + 14] + [58 + 54 + 11] = 245.

Возможно, это обстоятельство призвано было отразить идею едва заметного нарушения числовой гармонии, композиции, когда несоответствие сводится к минимуму. Однако при условии, когда двойная лунка с принимается за 1, количество знаков в центральной спирали и во всех периферийных структурах выравнивается:

242 + 1 + 1 = 244,

[62 + 45 + 14] + [58 + 54 + 11] = 244.

Нетрудно заметить и такую примечательную деталь: при последнем условии общее количество знаков в структурах левого и правого отделов композиции оказывается близким половине количества знаков центральной спирали. Но в первом случае для такого сопоставления недостает одного знака:

62 + 45 + 14= 121,

а в другом обнаруживается такое же превышение:

58 + 54+ 11 = 123.

Подводя итог анализу, можно предположить следующее: на мальтинской пластине из бивня мамонта посредством лунок и сквозного отверстия зафиксирована комплексная информационная система, отдельные структурные части которой характеризуются числовой неопределенностью. Это возможное колебание (в пределах 1–2 единиц) общего числа знаков в таких структурах, позволяющее, очевидно, выбрать варианты при счислении по ним, обусловлено остроумным введением в систему двойной лунки с, размещением лунок о и р за пределами резных линий и наличием сквозного отверстия а, как особого знака.

Внимание привлекает также разнонаправленность витков в периферийных спиралях: расположенные напротив друг друга слева и справа относительно центральной фигуры спирали 62(63) и 57+1, 45 и 54 закручены противолежаще, что выразительно противопоставляет левый и правый отделы композиции. Эта броская особенность, как можно догадываться, знаково-информационная по сути своей, требует нетривиальной интерпретации, что и будет осуществлено далее при решении еще одной, не менее занимательной задачи: почему при близости количества знаков в структурах левого и правого отделов композиции (около 122) число знаков в противопоставленных (относительно центра) спиральных и иных фигурах разнится столь очевидно:

62(63) ? 57 + 1,

45 ? 54,

14 ? 11.

Целенаправленный отбор количества лунок для каждой части орнаментальной композиции пластины подтверждается при реконструкции счисления времени в течение тропического года с условием, что каждая лунка обозначает одни сутки. Предполагается, что счет велся по двухлетиям с поочередным подключением к центральной спирали 242 + 1 сначала узоров левой периферии, затем правой.

Схема записи первого тропического года:

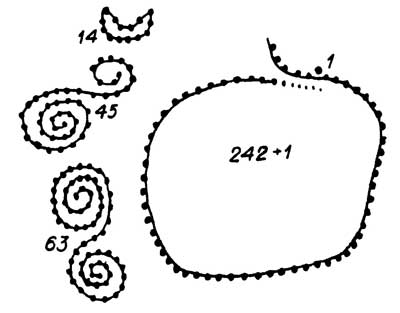
242 + 1 ? 63 ? 45 ? 14 = 365

Схема записи второго тропического года:

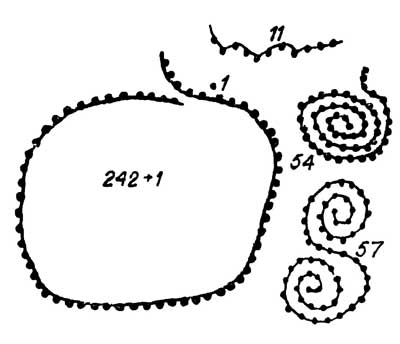
242 + 1 ? 57 ? 54 ? 11 = 365.

Рациональность такого порядка счета времени с помощью знаков спиральных блоков, каждый из которых в отдельности обязательно кратен трем[28], можно подтвердить следующими соображениями.

Если за начало отсчета принять соседнюю со сквозным отверстием лунку центральной спирали и условиться, что она есть день летнего солнцестояния, то это позволит определить очень заметную позицию знака, обозначающего день зимнего солнцестояния. Оно придется на лунку, на которой завершается раскрутка внутренних витков центральной спирали и начинается отсчет времени по внешнему ее витку (здесь находится выход из круговертей спирали). В таком случае на последнюю лунку внешнего витка центральной спирали придется начало последней декады февраля, как раз тот знаменательный момент, когда после 60 суток со дня зимнего солнцестояния вечером восходит Арктур, знаменующий приближение весны.

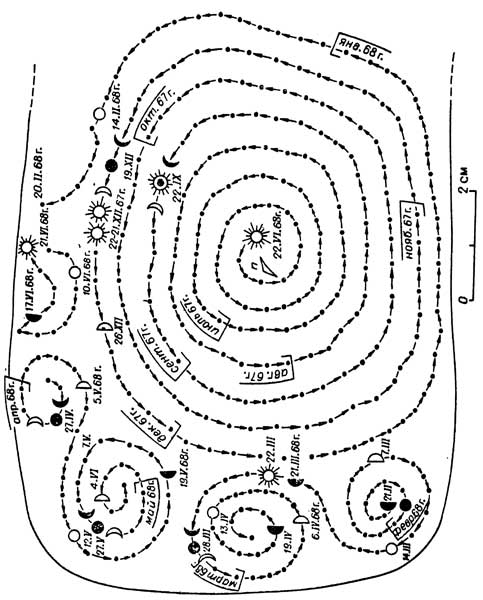
Схема наложения астрономического календаря от 22 июня 1967 года по 21 июня 1968 года на знаковую систему центральное спирали и структур левой периферии мальтинской пластины.

Число лунок в центральной спирали (243) примечательно и тем, что близко наименьшему целому числу дней между, скажем, двумя минимумами скорости перемещения Луны по небосводу (так называемая зигзагообразная функция). Такой календарный блок, важный для предсказания затмения, покрывает около девяти колебаний скорости Луны или почти девять аномалистических месяцев (уравнение, исток которого возводился ранее к астрономии времен античности). Число лунок в этом блоке близко продолжительности девяти сидерических месяцев, что важно для выявления методов наблюдения за Луной в эпоху палеолита (можно говорить о точной фиксации перемещений ее на фоне звезд, а не просто о слежении за фазами, достаточном при синодическом счислении времени). О том же самом свидетельствует количество лунок в периферийных узорах как левой, так и правой окраин пластины. Их число в том и другом случае соответствует длительности в сутках 4,5 аномалистического или сидерического месяцев, а вместе — 9, то есть их столько же, сколько в лунках центральной спирали. Это стремление выделить в тропическом (солнечном) году лунные циклы представляется чрезвычайно важным для определения истинного характера календаря.

При счислении времени по знакам нижних боковых спиралей весьма заметными оказываются позиции лунок, определяющих момент весеннего равноденствия (знаки между закрученными в разные стороны витками спиралей 62(63) и 57 + 1), а также одного из важнейших подразделений майского календаря, границы которого приходятся на 5–7 мая (лунка между закрученными в разные стороны витками спирали 45 и лунка входа в лабиринт внутренних витков спирали 54). Что касается отражений в этих блоках счисления времени по лунному календарю, то обращает на себя внимание кратность синодическому счислению времени по лункам спиралей 62(63) и 57 + 1, расположенных в нижнем отделе пластины, и сидерическому по лункам спиралей 45 и 54, расположенных в верхнем ее отделе. Не есть ли это свидетельство того; что для моментов весеннего равноденствия существенную роль играла прежде всего фаза Луны, а для промежуточных рубежей майского календаря, как и во времена Гесиода, — положение ночного светила среди звезд (восход или заход их)?

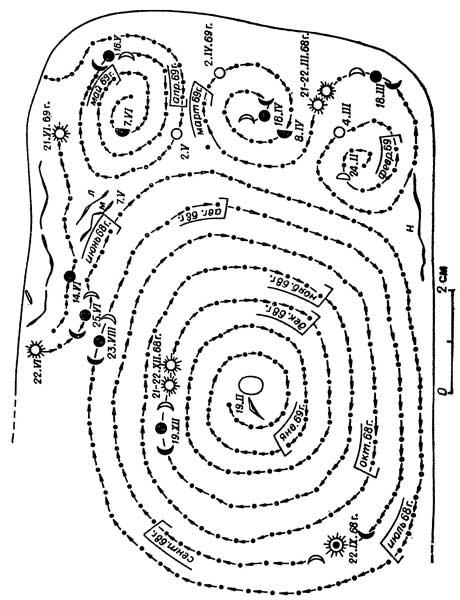
Схемы наложения астрономического календаря от 22 июня 1968 года по 21 июня 1969 года на знаковую систему центральной спирали и структур периферии мальтинской пластины.

В любом случае в солнечном календаре мальтинской пластины с достаточной очевидностью просматриваются признаки календаря лунного, и это весьма существенная деталь. Она, возможно, раскрывает признаки оригинального, не имеющего аналогов, комбинаторного счисления времени, когда счет его велся в течение года в основном по Солнцу, а слежение по месяцам за Луной, как и в случае со знаковой системой ачинской скульптуры, поочередно было то сидерическим, то синодическим. Если это так, то становится понятным, почему, допустим, неодинаковое количество лунок включалось в спирали 62(63) и 57 + 1, хотя та и другая призваны были наглядно представить позиции весеннего равноденствия. Все дело в том, что превышение на трое суток двух синодических месяцев в первом году удовлетворительно компенсировалось недобором их при счислении второго года. В самом деле,

63: 29,5306 = 2,1333,

57: 29,5306 = 1,9302.

При таком варианте расшифровки записей остается убедительно ответить на вопрос: что предопределяло включение различного количества лунок в структуры левой и правой периферий орнаментальной композиции пластины, если продолжительность тропического года была известна палеолитическому человеку Сибири с точностью до суток? Не проще ли было ограничиться выбором одного из приведенных выше вариантов годового счисления времени по Солнцу? Разумеется, проще. Если бы не было острой необходимости следить одновременно и за Луной.

Бросается в глаза весьма примечательное обстоятельство: блоки лунок в структурах позволяют получать характерные календарно-астрономические записи.

Лунный год, как известно, составляет 354,36706 суток; он записан знаками центральной спирали и спиральных узоров правой периферии пластины:

242 + 1 ? 57 ? 54 = 354. Каждый из блоков этой системы кратен трем.

Можно «прочесть» и календарный период, на который тропический год, представленный, положим, центральной спиралью и узорами левой периферии пластины, отличается по продолжительности от лунного и наоборот, — 10,875 суток. Схема его записи — змеевидная линия с 11 лунками правой периферии пластины.

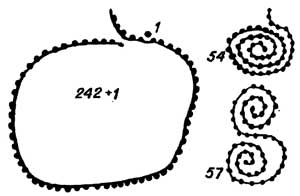
Схема записи лунного года.

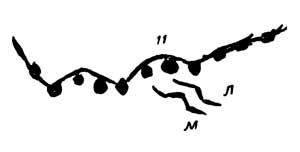
Схема записи календарного периода, на который тропический год отличается от лунного.

Если к этим двум записям добавить третью — приведенную выше запись первого тропического года, то, как нетрудно заметить, они исчерпывают орнаментально-числовые структуры пластины полностью. Примечательно, что при подобной комплексной по характеру реконструкции центральная спираль используется дважды — в сочетании ее со всеми структурами левой периферии ведется счет по Солнцу (242 + 1 + 63 + + 45 + 14 = 365), а в сочетании только со спиральными структурами правой периферии — по Луне (242 + + 1 + 57 + 54 = 354).

Неиспользованными остаются лунки змеевидной линии 11, как бы наглядно демонстрируя, на какой календарный период тропический год отличается от лунного. При таком понимании структуры орнамента мальтинской пластины приобретает особый смысл счисление по узорам левой или правой периферий ее, как и направленность (по часовой или против часовой стрелки) витков в спиралях, расположенных напротив друг друга по обе стороны от спирали центральной, слева и справа от нее. Проход по лункам структур центра и левой части композиции с соответствующим направлением витков спиралей мог означать счисление времени по Солнцу, а структур центра и правой части композиции с противоположной ориентацией витков — по Луне. Трехкратный проход по всем 487 лункам позволяет с удовлетворительной точностью выразить продолжительность тропического четырехлетия, что, возможно, приоткрывает завесу над способом решения палеолитическим человеком проблемы високоса:

365,242 4 = 1460,968 суток, 487 • 3 = 1461 сутки.