Радость познания

Радость познания

Урок, который описываю ниже, можно провести в курсе математики в III–IV классе. Главная цель урока — приобщить детей к поисковой деятельности. Но так как урок является одним из звеньев в цепи уроков, то продолжается и решение других задач: через учительское общение утвердить в детях радость познания, помочь им дальше развить умение мыслить сосредоточенно и целенаправленно, применять способы анализа и синтеза, догадливость и выдвижение гипотез и т. д.

«Волшебный (магический) квадрат» Альбрехта Дюрера, немецкого художника, мыслителя и гуманиста (годы жизни 1471–1528), дает прекрасную возможность, чтобы восхитить детей, увлечь их и на основе скрытых мотивационных устремлений помочь им закрепить в себе разные математические и мыслительные операции. Действительное «волшебство» квадрата вызывает в детях живой интерес к разгадке способа («тайны») его составления. Детям предлагаю войти в роль исследователя, стать научным сотрудником исследовательской лаборатории, стать коллегами друг для друга и совместными усилиями решить «научную проблему» — открыть тайну средневекового гуманиста и художника, которую он заключил в своем увлекательном квадрате.

Урок я веду в духе сотрудничества с детьми и уважения личности каждого из них, поощряю их коллегиальную взаимность в работе и сорадуюсь в связи с успехом товарища в поиске и восхождении мысли. На уроке я вхожу в роль тоже «ищущего»: «путаюсь», «догадываюсь», «ошибаюсь», радуюсь. Ставлю себя на равноправных началах со всеми. Моя скрытая ведущая роль заключается именно в том, как и в чем буду «ошибаться», о чем буду «догадываться», как буду выражать «недоумение» и, наконец, как вместе с детьми буду радоваться победе.

Есть еще одна тонкость, которую я постоянно имею в виду: ведь может случиться, что тайну Альбрехта Дюрера кто-то из современных вундеркиндов откроет сразу, и что же тогда будет, ведь урок уже не состоится? И не состоится потому, что для меня главным является не сама «тайна», а организация ее устремленного, напряженного поиска. Как быть с таким вундеркиндом или просто догадливым ребенком? Конечно, урок провалится, если я буду вести его традиционным способом: скажу детям, что бы подняли руки, кто догадался, и сразу дам возможность первому же «открывателю» ответить. Чтобы и вундеркинд смог утвердить себя, и у всех остальных была возможность развиваться, я воспользуюсь на уроке приемом «нашептывания». Это означает: что каждый, чтобы не мешать остальным думать, будет мне шепотом объяснять свою версию. «Вундеркинду» я выскажу «сомнение» и попрошу, чтобы тот перепроверил свою версию, «ввергну» в заблуждение, то есть, усложню задачу, а потом, когда он еще больше убедится в своей правоте, извинюсь перед ним, скажу, что, конечно, он прав, я ошибался, пожму ему руку, порадуюсь и т. д. Таким образом, задачу буду «держать» до тех пор, пока я не исчерпаю ее педагогические возможности в пределах урочного времени.

Разгадка тайны вызовет общий восторг, я приложу усилия, чтобы это стало общим праздником, радостью познания; покажу всем, что надо уважать открывателей (такими окажутся двое-трое), но эти открыватели со своей стороны поймут, что без участия других, без общих усилий им было бы трудно достичь успеха.

После разгадки тайны детям захочется создать свой волшебный квадрат, и можно будет потом, спустя несколько дней, устроить в школе выставку красочно разрисованных и оформленных волшебных квадратов. Можно поощрить детей продолжить исследование квадрата: по какому порядку закладывается сумма чисел в нем. Так дети увидят и «строптивость» квадрата.

На доске я заранее записываю и зарисовываю нужный материал. Он состоит из трех групп: чтобы настроить детей принять на себя роль исследователя, чтобы подготовить их к решению задачи, а потом сам волшебный квадрат. Забочусь о том, чтобы материал на доске выглядел заманчиво и красиво, применяю цветные мелки. Каждое задание и каждую запись отделяю друг от друга, они должны быть выполнены крупно, чтобы с любого места дети видели и воспринимали их без напряжения зрения.

Записи на доске

УРОК: Тайна Альбрехта Дюрера,

немецкого художника, мыслителя, гуманиста

(годы жизни 1471–1528)

Эта запись делается на самом верху доски.

МЫ НАУЧНО-

И ИССЛЕДОВАТЕЛЬСКАЯ

С ЛАБОРАТОРИЯ

С

Л КОЛЛЕГИ

Е

Д

О

В

А

Т

Е

Л

И

Эта запись занимает левую часть доски. Ее можно дать и в другой форме:

мы

ис

— след-

ователи

научная

лаборатория

коллеги

В центральной части доски размещается сам квадрат, крупно, красочно, загадочно. Желательно, чтобы он был закрыт или занавеской, или краями доски, если доска открывается.

В О Л Ш Е Б Н Ы Й

А 16 3 2 13 К

Л В

Ь 5 10 11 8 А

Б Д

Р 9 6 7 12 Р

Е А

Х 4 15 14 1 Т

Т

Д Ю Р Е Р

С правой стороны доски записываются подготовительные задания:

1. { ?,? Ш, , А, }

2. { 9, 1, 23, 15, 7, 2, 31, 6, 4, 96 }

3. 19, 28, 37, ?,?, ?, ?, ?, ?

3

4 9

5 7 8

Ход урока

Условные обозначения:

«—» — учитель, «=» — ребенок, дети.

Задаю детям доброе и рабочее настроение.

— Здравствуйте, ребята!

= Здравствуйте!

— Какое у вас настроение сегодня?

= Хорошее… Бодрое… Отличное…

= А у вас?

— Я волнуюсь!

= Почему?

— Потому что задумал урок, в котором хочу пригласить вас стать исследователями. А какой получится урок, не знаю!

= Почему не получится?.. Получится!..

— Но вот в чем дело: задачу, которую хочу задать вам, я сам решить не смог…

= Что за такая задача?

— Вот, посмотрите…

Открываю центральную часть доски.

— Это…

Показываю на запись по углам квадрата. Дети читают:

= «Волшебный квадрат. Альбрехт Дюрер».

= Кто он, Альбрехт Дюрер, и в чем тайна квадрата?

— На днях, работая в библиотеке, в одном журнале я наткнулся на этот, правда, удивительный квадрат с цифрами. Создал его немецкий художник, мыслитель, гуманист Альбрехт Дюрер примерно пятьсот лет тому назад. Квадрат называется волшебным, магическим. Потом я объясню, почему. Я много старался, но открыть тайну, по которой составлен квадрат, не смог. И вот рискнул исследовать его с вами вместе. Если, конечно, вы согласны.

= Согласны…

— Вы поможете мне?

= Поможем… Интересно…

— Тогда я вам предложу план нашей работы. Он такой: сперва разобраться в вопросе и настроить себя на исследование, потом проверить и сосредоточить наши силы, а потом лишь приступить к исследованию квадрата. Я думаю, так будет лучше, ибо задача сложная. Согласны на мой план?

= Да…

— Давайте тогда начнем. Посмотрите, как я записал на доске слово «исследователи».

= Вы выделили в слове «след».

— Это нам поможет понять, что значит исследовать.

= Обнаружить след…

= Идти по следу…

= Найти след… А исследователь будет тот, кто ищет след чего-либо или кого-либо…

= Ис-след-овать, значит понять, установить…

= Ученые исследуют, изучают… исследуют природу…

= Исследование дает знания, точные знания…

— Они называются истинами, законами…

= Да…

— Я понял, что вам ясен смысл исследования. Мне понравилось и определение — «найти след». Так вот, в волшебном квадрате Альбрехта Дюрера нам придется найти след его тайны. Я предлагаю вам следующее: превратим наш класс в научно-исследовательскую лабораторию, каждый из нас — сотрудник этой лаборатории, ученый-исследователь. Мы все равны. Я записал вам здесь еще одно слово (показываю на доске).

= «Коллеги».

— Знаете это слово?

= Я слышал в одном фильме, как врач говорит врачу — коллега, и подумал, что это его имя.

— Коллега — значит товарищ по работе, по профессии. Мы — все сотрудники, ученые-исследователи лаборатории, мы — коллеги друг для друга. Будем работать коллегиально, то есть дружески, с уважением друг к другу. Я зарисовал на доске еще несколько рамочек. Попытаемся определить те самые три-четыре качества, которые будет проявлять каждый из нас, как ученый-исследователь. Подумайте сперва.

После маленькой паузы.

= Самое главное — думать…

= То же самое хотел сказать…

— Согласен.

Пишу «думать» в первой рамке.

= Нужно будет сосредоточиться…

— Значит, сосредоточиться.

Пишу это слово в следующей рамке.

= Анализировать.

= Обобщать.

= Разобраться.

= Догадаться.

— Хотите назвать и другие важные качества?.. Все? Тогда, можно, я тоже назову одно важное для ученого качество? Быть устремленным. Вы принимаете это?

= Да.

— Без устремленности и воли можно забросить дело на полпути.

Все эти слова записываю в последующих рамках и под ними. На левой части доски появляется запись:

МЫ НАУЧНО-

И ИССЛЕДОВАТЕЛЬСКАЯ

С ЛАБОРАТОРИЯ

С

Л КОЛЛЕГИ

Е

Д

О ДУМАТЬ

В СОСРЕДОТАЧИВАТЬСЯ

А АНАЛИЗИРОВАТЬ

Т ОБОБЩАТЬ

Е НАБЛЮДАТЬ

Л РАЗБИРАТЬСЯ

И ДОГАДЫВАТЬСЯ

БЫТЬ УСТРЕМЛЕННЫМ

— Теперь сделаем маленькую паузу, чтобы каждый мысленно вообразил себя ученым-исследователем и призвал нужные силы. Скажите самому себе: «Я — ученый-исследователь, и мне нужно будет…»

Пауза, дети настраивают себя на сложную познавательную работу.

— Спасибо. А теперь проведем разминку наших сил и возможностей.

Обращаю внимание детей на правую часть доски.

— Здесь четыре разных задания. Начнем с первого — оно для проверки нашей наблюдательности и сосредоточенности. Вы готовы? Посмотрите внимательно на это множество и запомните все.

Указываю на первое задание.

Короткая пауза.

Потом быстро и энергично:

— Опустите головы… закройте глаза!..

В первое множество вношу изменения: в круге ставлю точку, в квадрате стираю точку, луч превращаю в отрезок, букву А превращаю в Д, равнобедренный треугольник делаю прямоугольным треугольником.

{ ?, ,? Ш, ?, Д, }

— Поднимите головы. Пусть каждый запишет себе на бумаге, что изменилось во множестве.

Короткая пауза.

— Ну как? Давайте проверим.

= Я заметил три изменения: в кругу появилась точка, точка исчезла в квадрате, буква А стала буквой Д…

= Я тоже три изменения обнаружила: точку в круге, луч превратился в отрезок, буква А стала буквой Д.

= Я целых четыре изменения обнаружил: точку в круге, исчезновение точки в квадрате, букву Д вместо буквы А и отрезок, который был лучом.

= Есть еще и пятое изменение: треугольник, который был равнобедренным, стал прямоугольным.

— Думаю, там еще одно изменение.

В действительности шестого изменения во множестве нет. Дети внимательно смотрят на задание.

= Там нет других изменений.

= Только пять… нет других.

— Простите, ребята, наверное, я ошибся… А теперь второе задание. Здесь нужна ваша большая сосредоточенность и память. В этом множестве (показываю второе задание на доске) десять чисел, совершенно беспорядочно расположенных. Даю вам десять секунд на запоминание всех чисел.

Пауза.

— Кто готов?

Приглашаю пять ребятишек, ставлю их спиной к доске и прошу назвать числа последовательно.

= 9, 1, 23, 15, 2…

Один замешкался.

Пробует другой.

= 9, 1, 23, 15, 7, 2… 4…

= 9, 1, 23, 15, 7, 2, 31…

= 9, 1, 23, 15, 7…

= 9, 1, 23, 15, 7, 2, 31, 6, 4…

Дети аплодируют.

Приглашаю следующую пятерку.

Некоторые ошибаются, но двое называют все числа. Им тоже аплодируем.

— Переходим к третьему заданию. Тут нам понадобятся все лучшие качества исследователя: думать, догадываться, анализировать, обобщать. В этом числовом ряду заложен определенный порядок. Надо открыть его и завершить ряд пропущенными числами. Уважаемые коллеги, решайте, пожалуйста, задачу, а ваш ответ шепните мне на ухо.

Даю детям возможность подумать.

Саша поднял руку, зовет к себе.

= Каждое последующее число больше предыдущего на 9, поэтому далее должны быть числа 46, 55, 64, 73, 82 и 91. Так? — шепчет мне мальчик на ухо.

— Коллега, перепроверь, пожалуйста, свою догадку. Ты говоришь «46»? Думаю, это не так. (Саша, конечно, прав, но я завышаю ему умственную планку: пусть сам убедится, что прав).

Зовет Алина.

= Первые цифры в числах увеличиваются на один; посмотрите: 19, 28, 37 и т. д., 1, 2, 3, 4 и так до 9… — шепчет мне девочка.

— А дальше?

= А вторые числа уменьшаются тоже на один: 9, 8, 7, 6, 5, 4…

— И что из всего этого вытекает?

= Значит, там должны быть числа 4 и 6, 5 и 5, 6 и 4, 7 и 3, 8 и 2, 9 и 1… Правильно?

Я жму девочке руку и шепчу: «Ты решила задачу необычно, но правильно. Есть еще и другое решение. Найди его».

Меня зовут уже многие.

Саша сам спешит ко мне:

= Я прав, 73, 82, 91… Других чисел не может быть.

— А как я тебе сказал?

= Вы сказали, что 46 неправильно.

— Прости, пожалуйста, коллега, я ошибся. Конечно, ты прав! — Жму руку мальчику и шепчу, — Задача имеет и другое решение. Найди его.

Вот Мика.

= В каждом числе сумма цифр составляет 10. Вначале берется самое большое и самое малое значение цифр 9 и 1, потом 8 и 2 и т. д. После 55 положение цифр в числах меняется: было, скажем 4 и 6, а потом 6 и 4. Потому продолжением будут: 7 и 3, т. е. 73, 8 и 2, 82, 9 и 1, 91. Так ведь?

Жму руку мальчику.

— Ты меня удивил своей догадкой. Я и не думал, что задачу можно решать так. Спасибо. Найди теперь другой способ решения.

Я пошептался с большинством детей: кому-то помогаю, намекая на возможное увеличение последующего числа на постоянную величину; кого-то ввожу в заблуждение, говорю, что тот допускает такую-то ошибку (потом этот ребенок, убедившись в своей правоте, объясняет мне, что прав он, а не я, и я соглашаюсь); кому-то жму руку и тут же предлагаю найти другой способ решения. Делаю это в зависимости от возможностей каждого ребенка.

Подытоживаем результаты усилий.

Дети видят, что задача была решена тремя способами, и в каждом случае ряд чисел завершался числами 73, 82, 91.

— Таким образом, какие исследовательские умения помогали нам решать задачу?

= Думание… Сосредоточенность… Сообразительность… Догадка…

— А теперь последнее задание, которое приблизит нас к волшебному квадрату. Тут понадобятся нам все исследовательские умения. Вы готовы, коллеги, принять задание?..

= Да!

— Прошу полного внимания.

Объясняю задание медленно и разборчиво, акцентирую его основные условия.

— Вот схема из шести квадратов, и вот шесть чисел. Числа эти надо расположить в квадратах так, чтобы сумма каждых двух чисел по вертикали была одинаковая, а сумма трех чисел по горизонтали была в два раза больше суммы трех чисел второй горизонтали. Есть у вас, коллеги, вопросы ко мне?.. Нет?.. Тогда приступим к делу.

Мое объяснение сопровождается дополнительными знаками на схеме, которая принимает на доске следующую форму:

3

4 9

5 7 8

Время на задание ограничено — три с половиной минуты. В классе воцаряется полная тишина, «шуршит» только напряженная мысль детей.

Медленно передвигаюсь по рядам.

Шепчу Диме: «Как приятно смотреть на тебя, погруженного в мысли!»

Шепчу Кате: «Ты сегодня удивляешь меня. Спасибо».

И говорю полушепотом всем: «Как прекрасно, когда в лаборатории царствует мысль. Спасибо, ребята, мне так хорошо с вами!»

Вот и первые зовы.

Это Гога:

= Если числа расположить так, то суммы будут 12 и 24.

Схема у него заполнена так:

3 4 5 12

9 8 7 24

12 12 12

Выражаю радость.

— Спасибо… Прекрасно! — жму руку Гоге.

Это Таня.

= Вот что у меня получается, — и показывает свою схему, — но вы сказали, что сумма одних горизонтальных чисел должна быть в два раза больше суммы других горизонтальных чисел. А у меня суммы получились равными.

8 3 7 18

4 9 5 18

12 12 12

— Коллеги, я и не предполагал, что задачу можно решить так! Может быть, я ошибся? Проверь, пожалуйста, и попытайся переставить числа.

Это Илья. Показывает схему и морщится.

7 9 4 20

5 3 8 16

12 12 12

— Думаю, если переставить числа, все будет в порядке.

Наконец, с задачей справились все, и схема на доске приняла вид:

3 4 5 12

9 8 7 24

12 12 12

— Таким образом, мы отточили наши исследовательские способности. Как решать эти задачи, я, конечно, знал, но открыть тайну волшебного квадрата я не смог. Предлагаю вам этот удивительный квадрат Альбрехта Дюрера для коллективного исследования.

Открываю центральную часть доски.

— Посмотрите, как он красив… Попытайтесь сперва раскрыть, в чем его волшебство.

Дети внимательно всматриваются в квадрат на доске.

Майя:

= Сумма чисел по горизонтали одинакова — по 34.

— Только по горизонтали?

Владик:

= По вертикали сумма чисел тоже 34.

— Проверьте, пожалуйста.

Дети убеждаются, что это так.

— Но только по вертикали и горизонтали?

Мика:

= Ой, ой, по диагонали тоже: 16, 10, 7, 1 — будет 34; 4, 6, 11, 13 — тоже 34.

— Значит, по горизонтали, по вертикали, по диагонали сумма чисел одна и та же — 34… Исследуйте дальше, коллеги.

Дети открывают, что если разделить квадрат на 4 равные части, то в каждой части сумма чисел опять будет 34 (16+3+5+10; 2+13+11+8; 9+6+4+15; 7+12+14+1).

Саша:

= Я еще нашел. Посмотрите на средние числа: 10, 11, 6 и 7, их сумма тоже 34.

— Спасибо, коллега, я этого не заметил, когда изучал квадрат. Продолжайте исследование квадрата.

Дети постепенно открывают разные свойства квадрата и все больше удивляются его необычности.

Лена:

= Числа, которые… — девочка не может словами сказать их места, поэтому показывает, — вот, 5, 10, 9, 6, или же 3, 2, 10, 11, потом 11, 8, 7, 12 и 6, 7, 15, 14 в сумме не дают 34… Но если брать так: 5, 9 и 8, 12, будет 34, также 3, 2 и 15, 14, тоже 34.

Иван:

= А я другое нашел: 16, 5 и 13, 8 дают одинаковую сумму — 21; а 9, 4 и 12, 1 тоже одинаковую — 13. Потом 16, 3 и 4, 15 — тоже одинаковая сумма — 19; а потом 2, 13 и 14, 1 будет 15,

Нина:

= Посмотрите, как интересно: крайние угловые числа — 16 и 1 и 13 и 4, а также числа, которые на перекрестке — 10 и 7 и 6 и 11, всюду в сумме дают 17.

— Все, о чем вы сейчас говорите, ново для меня. Я только знал о сумме 34. А вы открываете и другие прелести этого квадрата. Он нравится вам?

= Да… очень интересный квадрат…

= Настоящий волшебный квадрат…

— Видно, его свойства можно исследовать долго. Но давайте, коллеги, перейдем на самое главное: по какому принципу построен этот квадрат. Иначе, какую тайну заключил Альбрехт Дюрер в своем удивительном квадрате. Вот эту тайну я не смог разгадать. Но она тут, перед нашими глазами, в самом квадрате. Если мы откроем тайну, то каждый сможет построить свой волшебный квадрат. Можете срисовать квадрат на бумагу. Значит, исследуем тайну — способ построения квадрата. Призовем все свои исследовательские способности…

= Думать, анализировать, обобщать, проникать…

— Если хотите, можете исследовать тайну вдвоем, втроем или в одиночку… Через несколько минут обсудим версии, к которым вы придете…

Пауза.

Я подхожу к Дмитрию и предлагаю подумать вместе.

Дмитрий:

= Если каждое число в квадрате удвоить или утроить, то получится новый квадрат.

— Но это же не тайна… Нам надо понять, как, в каком порядке, в какой последовательности расположены числа в квадрате.

Дмитрий думает.

= Смотрите, что я нашел, может быть, тут тайна? Вот в средних столбиках рядом стоят порядковые числа: 3 и 2, под ними 10 и 11, под ними 6 и 7, а потом 15 и 14.

— Это интересно… Дальше след теряется… Может быть, есть какой-либо порядок в столбиках?

После размышлений:

= Нет никакого порядка… тоже след исчезает.

Вадим с двумя товарищами:

= У нас сложилась версия.

Обращаюсь ко всем:

— Коллеги, давайте обсудим версию группы Вадима.

Вадим:

= Посмотрите, мы заметили такое расположение одной группы чисел. Берите средние два столбика: разность соседних чисел в столбиках составляет 1.

3–2=1, 11–10=1, 7–6=1, 15–14=1.

Вопрос:

— А как с другими столбиками?

Вадим:

= Разность крайних чисел по горизонтали составляет 3; 16–13=3, 8–5=3, 4–1=3.

Вопрос:

= А вы пробовали составить новый квадрат таким же способом?

Вадим:

= Еще нет…

Андрей:

= Так у вас квадрат не получится.

Вадим:

= Почему?

Андрей:

= Не знаю, но уверен, что так Альбрехт Дюрер свой квадрат не строил. А вы все же попробуйте.

Обсуждаем другую версию.

Люба:

= А что, если воспользоваться тем, что говорит Нина? Крайние угловые числа и внутренние перекрестные числа (показывает на квадрате: 16+1, 4+13, 10+7, 6+11) дают в сумме 17.

Вопрос:

= Ну и что? Так тоже квадрат не построить…

Тимур:

= Я предлагаю не обсуждать такие версии — о суммах или разностях чисел. В новом квадрате, который мы хотим создать, числа изменятся, и сумма и разность их будут уже другие… Нам нужен общий способ.

Саша и Марика выдвигают свою версию.

Саша:

= Мы думаем, что напали на след. В квадрате 16 чисел, от 1 до 16 по порядку. Давайте посмотрим, как каждое последующее число расположено в квадрате. Вот 1, в самом нижнем правом углу, вот 2, в первом ряду в середине, тут же 3, а в самом нижнем углу слева — 4.

Реплика:

= Они так разбросаны… тоже нет порядка…

Марика:

= Почему? Давайте посмотрим дальше. Вот 5, вот 6, вот 7 и вот 8… тоже по какой-то схеме…

Вопрос:

= А дальше?

Саша и Марика замешкались.

Саша:

= Мы еще подумаем! — Саша с Марикой возвращаются на свои места.

Слушаю с подчеркнутой заинтересованностью тех, кто выдвигает версии. И хотя версия опровергается, я все же говорю авторам:

— Вы очень помогли нам… Значит, по этому пути ходить не будем… Спасибо!

Дети продолжают исследовать квадрат.

Арсений:

= Смотрите, что я обнаружил. Возьмем в квадрате числа вот так и сложим их: 16 + 10 + 11 + 13 и 4 + 6 + 7 + 1, сложим все вместе. Сколько будет? 68.

Реплика:

= А что это дает?

Арсений:

= Подожди. Возьмем по такой же схеме боковые числа: 16 + 10 + 6 + 4 и 13 + 11 + 7 + 1 и тоже все сложим вместе. Сколько будет? Опять 68.

Реплика:

= А как квадрат составить?

Арсений:

= Дело не в этом, а в схеме…

Реплика:

= Ты опять складываешь числа… Построй сперва по своей схеме квадрат.

Арсений:

= Но схема важна!

— Арсений, коллега, проверь свою схему.

Арсений:

= Я один не могу. Может быть, с вами вместе?

— Но я с Дмитрием работаю. Присоединяйся к нам.

Марина, возбужденно:

= Они же напали на след!..

= Кто они?

Марина:

= Саша и Марика. Они предложили правильный путь… И Арсений тоже догадался — нам нужна схема. А схему в квадрате я вижу.

— Марина, объясни, пожалуйста, о какой схеме ты говоришь.

Марина:

= Пусть Саша и Марика тоже подойдут к доске и помогут мне.

Дети все свое внимание переключили на Марину. К доске выходят Саша и Марика.

Марина:

= Беру красный мел, чтобы выделить схему. Посмотрите.

Волшебный квадрат на доске принимает следующий вид:

Марина:

= Видите, какая интересная схема, симметричная. Нам только надо знать эти линии от числа к числу, и получится новый квадрат.

Реплика:

= Ты так думаешь?

Саша:

= Получится, получится… Давайте вместе попробуем его составить.

Дети загорелись нетерпением.

Саша чертит на доске квадрат без цифр.

Саша:

= Назовите любое число, которое мы запишем вместо «1».

= Три… Пять…

Саша:

= Возьмем пять. Здесь пишем 5, идем по схеме — здесь — 6, рядом — 7, а в левом нижнем углу — 8. Дальше идем по другой схеме. Здесь пишем 9, здесь — 10, здесь — 11, здесь — 12. Затем третья схема. Получается — 13, 14, 15, 16. А потом четвертая схема: здесь 17, здесь 18, 19 и 20.

На доске рядом с волшебным квадратом Альбрехта Дюрера возникает новый квадрат:

20 7 6 17

9 14 15 12

13 10 11 16

8 19 18 5

Саша:

= А теперь давайте проверим.

В проверку нового квадрата включаются все.

Скоро выясняем, что сумма чисел во всех горизонтальных рядах и вертикальных столбиках равна 50.

Дети торжествуют.

= Открыли тайну… открыли тайну…

Я тоже не скрываю свои радость, восхищение.

— Ребята, не знаю даже, что сказать!.. Спасибо вам от имени всех ваших коллег, от себя…

Жму руку Саше, Марике, Марине.

= Арсению тоже пожмите руку.

— Арсений, выходи, пожалуйста! — жму руку.

Дети аплодируют им.

Марика:

= Открыли мы тайну все вместе… Когда Нина, Вадим и другие предлагали свои версии и показывали на квадрате числа, мы поняли, что нужно искать порядок в последовательности чисел…

— Марика права. Спасибо всем, коллеги, за сотрудничество, за усердие и устремление, за ваши мысли и творчество. Мы все вместе победили.

Дети опять аплодируют.

— Коллеги, чуть было не забыл. Есть еще одна тайна в квадрате. Ее то я открыл, но лучше будет, если вы откроете ее сами.

Дети стихают.

— В этом волшебном квадрате Альбрехта Дюрера записан год его создания. То, что вам нужно, чтобы догадаться, какой это год, написано на доске. Напомню только — XV–XVI века. Больше не скажу ни слова. Подумайте и предложите ваши версии.

Пауза. Напряженность мысли.

Предлагаются версии, я их записываю на доске.

= 1632 — первые четыре цифры.

= 1613 — угловые цифры верхнего ряда.

= 1610 — первые два числа по диагонали.

= 1514 — средние цифры в нижнем ряду.

= 1578… по диагонали…

В общем, на доске возникает столбик чисел:

1632

1613

1610

1514

1578

1659

1465

1516

1615

На этом все версии исчерпаны.

— Наверное, сперва надо исключить те версии, которые никак не могут быть обоснованы.

Анна:

= Альбрехт Дюрер жил в 1471–1528 годах. Это же на доске написано. Значит, не пригодятся версии: 1632, 1613, 1610, 1578, 1659, 1615. В эти годы его уже давно не было в живых. Не пригодится также 1465, ибо он еще не был рожден.

— Авторы этих версий согласны, или что-то имеют против?

= Вы же сказали, что он жил в XV–XVI веках…

Анна:

= Правильно… Но то, что превышает тысяча шестьсот, будет уже не шестнадцатый, а семнадцатый век.

= Ах, да…

— Тогда продиктуйте, пожалуйста, какие числа стереть…

Я стираю в столбике продиктованные числа.

— Значит, обсуждаем две версии: 1514 и 1516. Пусть обоснуют свои версии их авторы.

Женя:

= Я полагаю, что Альбрехт Дюрер, придумав такой красивый квадрат, дату его создания тоже красиво разместил бы в нем. 15 и 14 стоят рядом, в центре нижнего ряда чисел. Поэтому квадрат им был создан в 1514 году.

Рая:

= Я выбрала самые большие числа в этом квадрате, это 16 и 15, и, исходя из лет жизни, сложила из них 1516.

= Обе эти даты вероятны.

= Я все же думаю, что 1514 год — правильная дата. Она умело расположена в квадрате.

= Я тоже так думаю.

= А вы как думаете?

— Дата 1514, должно быть, более правильная. Альбрехт Дюрер был художником и, конечно, знал закон симметрии. Но я ценю сообразительность Раи… Таким образом, мы открыли и дату создания квадрата. Скажите, пожалуйста, вам понравился волшебный квадрат Альбрехта Дюрера?

Единогласно:

= Дааа…

— Что вы хотите о нем сказать?

= Квадрат составлен гениально…

= Квадрат восхитил меня…

= Квадрат — как философский камень, о котором вы говорили…

= Я полюбил волшебный квадрат…

= Спасибо волшебному квадрату, он сделал нас исследователями.

— Думаю, вам хочется встать и поклониться Альбрехту Дюреру, этому удивительному художнику и мыслителю, который оставил людям прекрасные картины, книги и этот волшебный квадрат!

Дети встают. Я тоже вместе с ними склоняю голову.

— Спасибо вам, коллеги… Вы очень помогли мне провести этот урок!

= Вам спасибо за интересный урок.

— Мы уже знаем способ составления волшебного квадрата. Если кто хочет, пусть составит свой квадрат; мы устроим выставку наших волшебных квадратов.

= Вы тоже сделаете?

— Конечно.

Урок закончен.

Дети собираются у доски, срисовывают схему, которую начертили Саша, Марика и Марина. У них получилась такая схема:

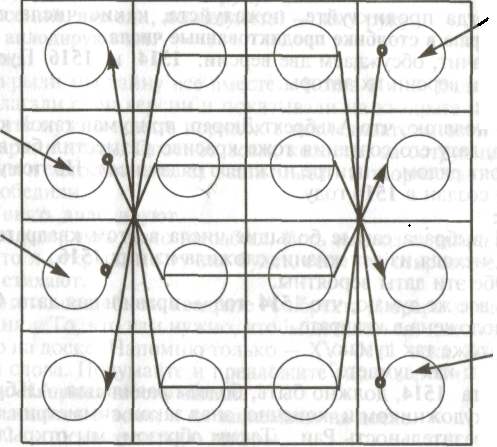
Заключение

Спустя несколько дней следует устроить выставку «Волшебных квадратов», составленных самими детьми и продолжить их исследование.

При этом важно, чтобы сам учитель так же проявил свою увлеченность и выставил свой новый квадрат.